CCA Stars Meeting Feb 7: Benjamin Pope

Total Variation Minimization Photometry

Benjamin Pope, NYU

CCA Stars Meeting

Feb 7 2018

Slides available at
benjaminpope.github.io/talks/ccafeb7/ccafeb7

Kepler Photometry

The Kepler Space Telescope, launched in 2009, looks for planets by the transit method, and also does asteroseismology.

After the failure of a reaction wheel in 2012, it is now operating as the 'K2 Mission', with very unstable pointing (hence the shaking in the videos you'll see).

To get the photometry, you can just sum the pixel values in a window containing the whole PSF...

but the pixels have different gains ("inter- and intra-pixel sensitivity variation")...

and the pixel window doesn't necessarily track the whole PSF perfectly ("aperture losses").

The EVEREST model (Luger et al, 2016) does 'pixel-level decorrelation', fitting a linear combination of pixel time series to the data, getting excellent photometry.

We will be motivated by this here.

For sufficiently bright stars, though, light fills the CCD wells with electrons that spill up and down the column, ruining the photometry as they leave the aperture.

Kepler saturates on stars brighter than ~ 11th mag (log scale: 5 mag = factor of 100) - but we want to look at stars 10k times brighter.

Halo Photometry

What if we just look at unsaturated pixels?

Flux \(f_i \) at cadence i is a sum over j pixels \(p_{ij}\) with weights \(w_j\):

\[ f_i \equiv \sum\limits_i w_j p_{ij} \]

In the OWL method (Hogg & Foreman-Mackey), you choose weights to minimize variance of the final light curve - but this has limited success.

To find the appropriate weights, we instead minimize the Total Variation

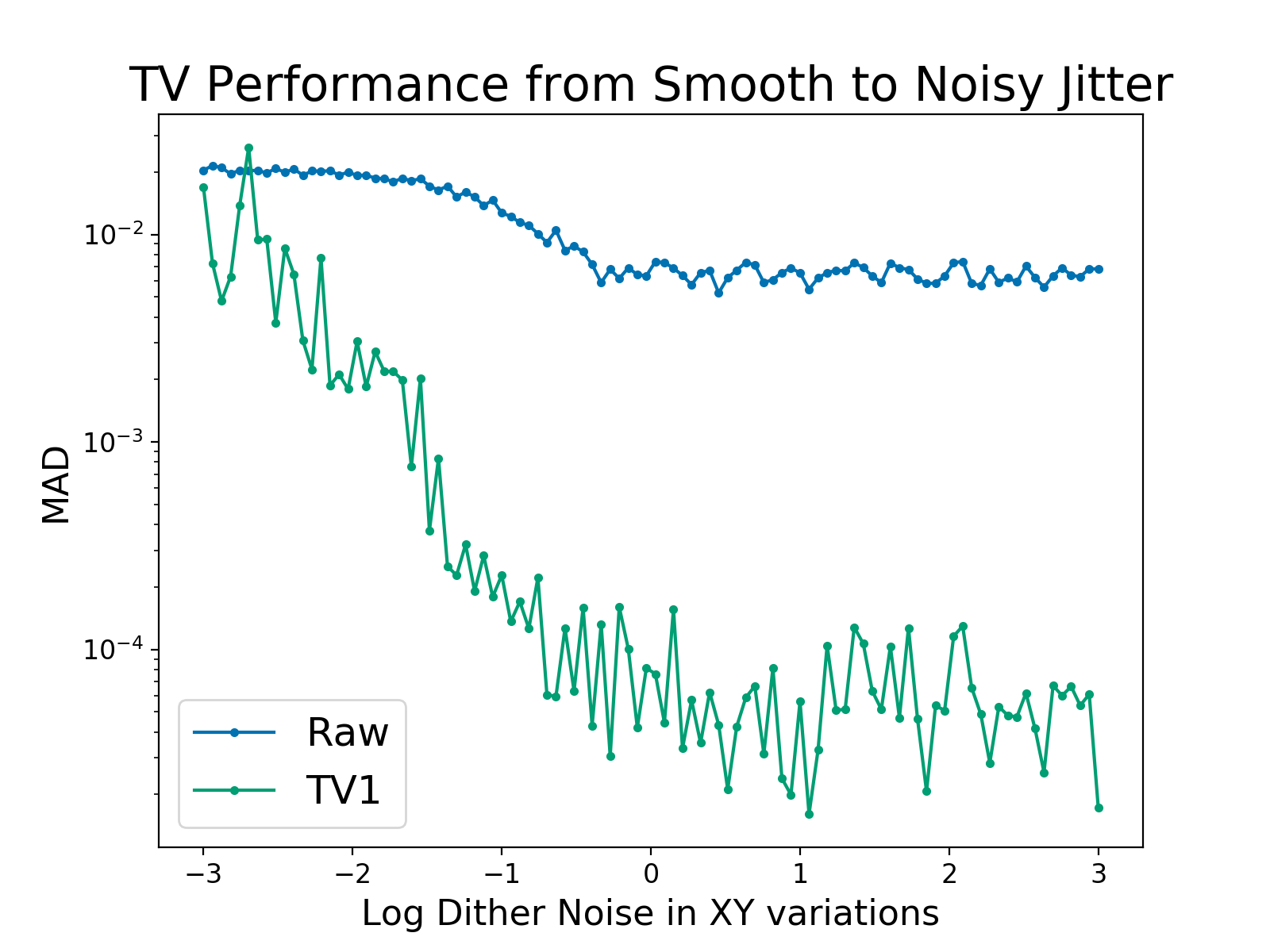
\[\begin{align} TV \equiv \dfrac{\sum_i |f_i - f_{i-1}|} {\sum_i f_i } \end{align} \]

This is the L1 norm on the derivative of the time series.

This has analytic derivatives in Theano - easy to optimize.

TV is widely used as a regularizer for reconstructing stepwise constant functions because it imposes sparsity on the derivative in a compressed-sensing framework.

Kepler light curves are not sparse in the derivative.

Note that these light curves are basically a sum of sine waves - anything but sparse in the derivative!

But they're sparse in the Fourier domain... perhaps this is relevant?

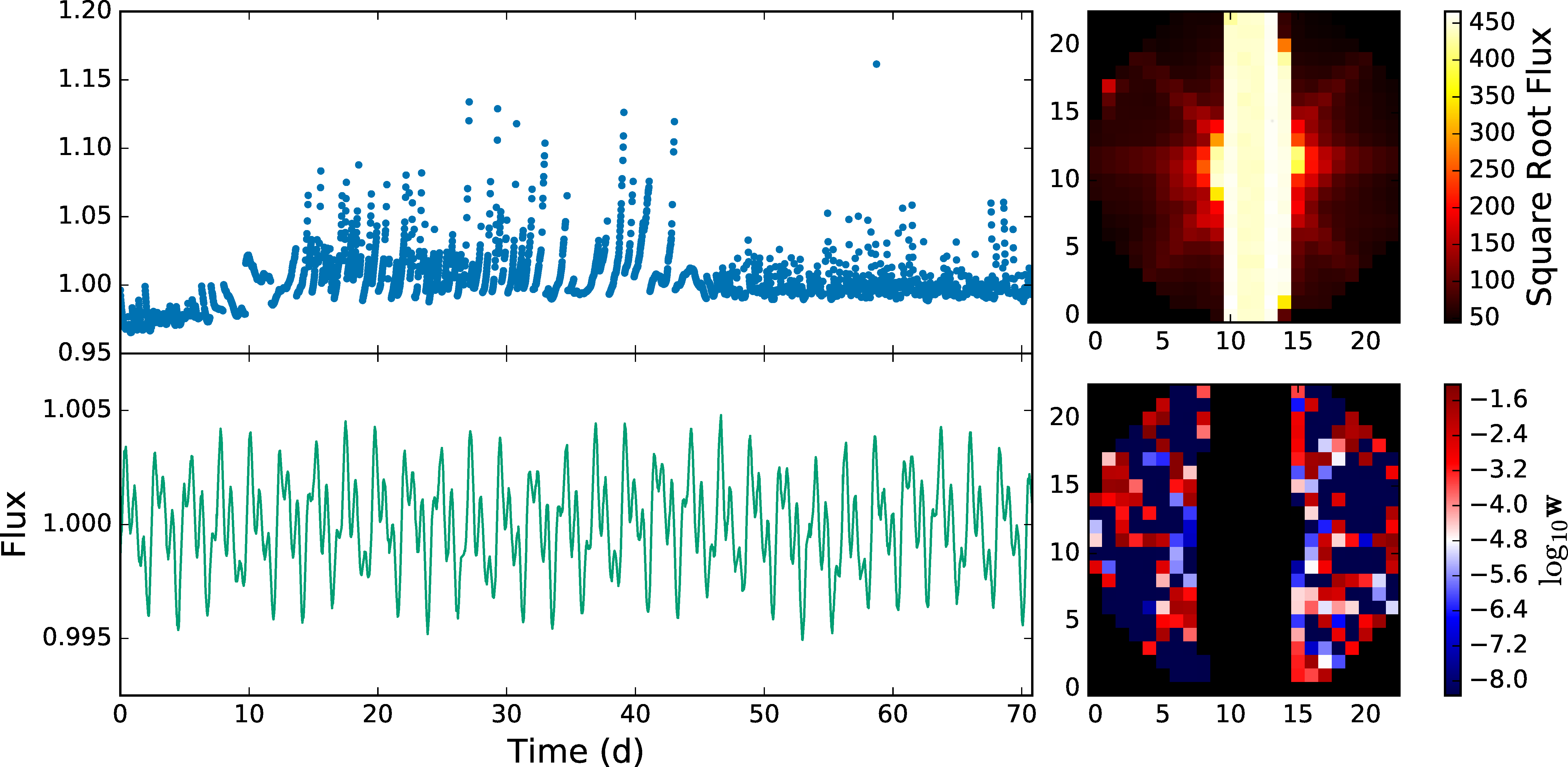
Atlas lightcurve: raw (top) and halo (bottom)

White, Pope et al., 2017

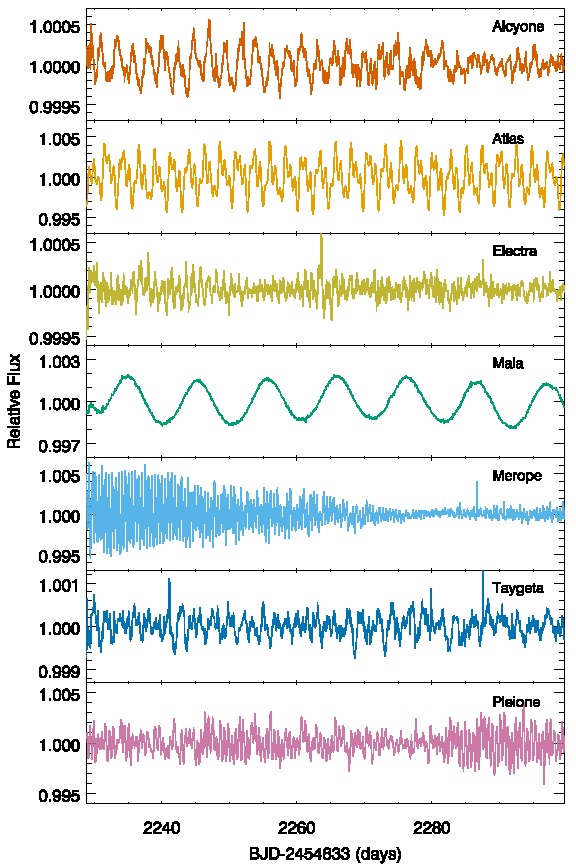
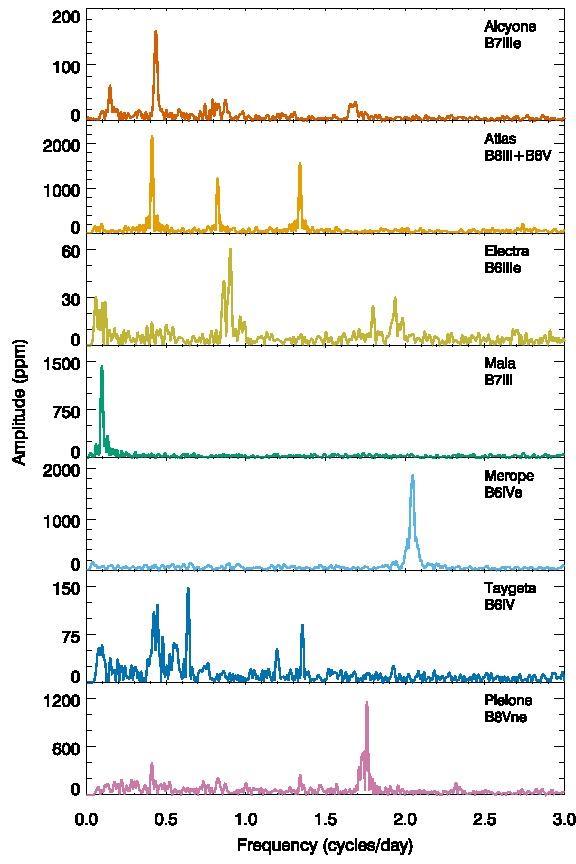
Lightcurves of All Seven Bright Pleiades

White, Pope et al., 2017

I have done some tests to examine why this works...

Tim White observed that short-cadence K2 data doesn't converge well, but if you train the weights on long-cadence data it applies well enough to short-cadence. (I don't have a figure for this, just Tim's comment).

I wanted to know if this was because of the level of correlation between adjacent datapoints, so I simulated some data. I moved the PSF around in a slow circle and simulated steadily increasing amounts of white noise on this while keeping the range constant, so that I could change continuously from very-correlated to uncorrelated positions.


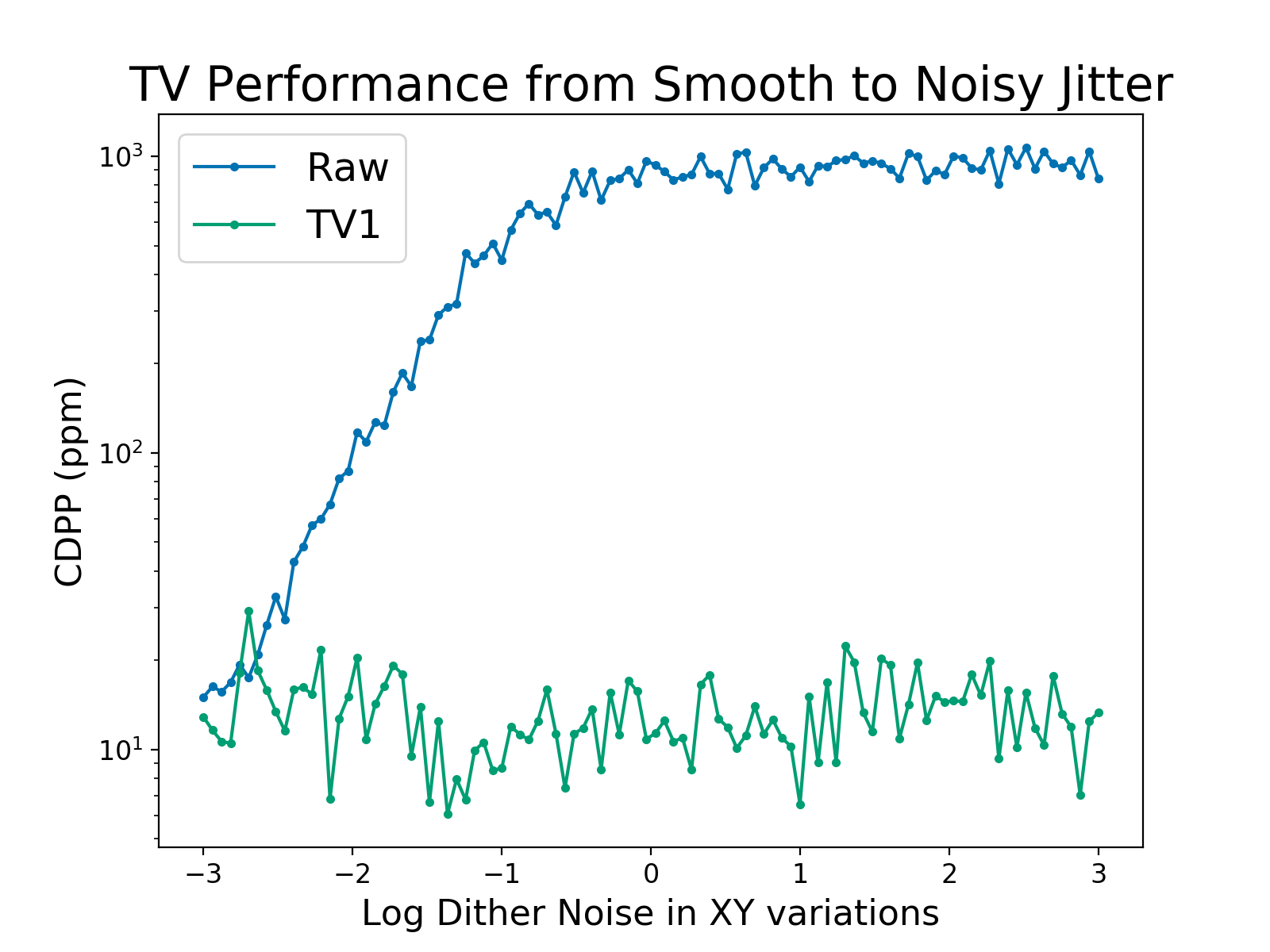
						x, y = np.sin(2*np.pi*t/20.), np.cos(2*np.pi*t/20.) # smooth
						f = 20*np.ones(ncad) + np.sin(t) 
						f[400:500] *= 0.9 # toy transit

						log_snrs = np.linspace(-3, 3,100)

						for jj, snr in enumerate(log_snrs):

							xx, yy = x + xamp*(10**snr)*np.random.randn(len(x)), y + yamp*(10**snr)*np.random.randn(len(y))

						### ... [guts of loop etc]

So total variation minimization works way better if you dither.

I wanted to check whether this was a frequency-dependent effect so I tried comparing a sinusoidal input light curve and sinusoidal xy with different frequencies.

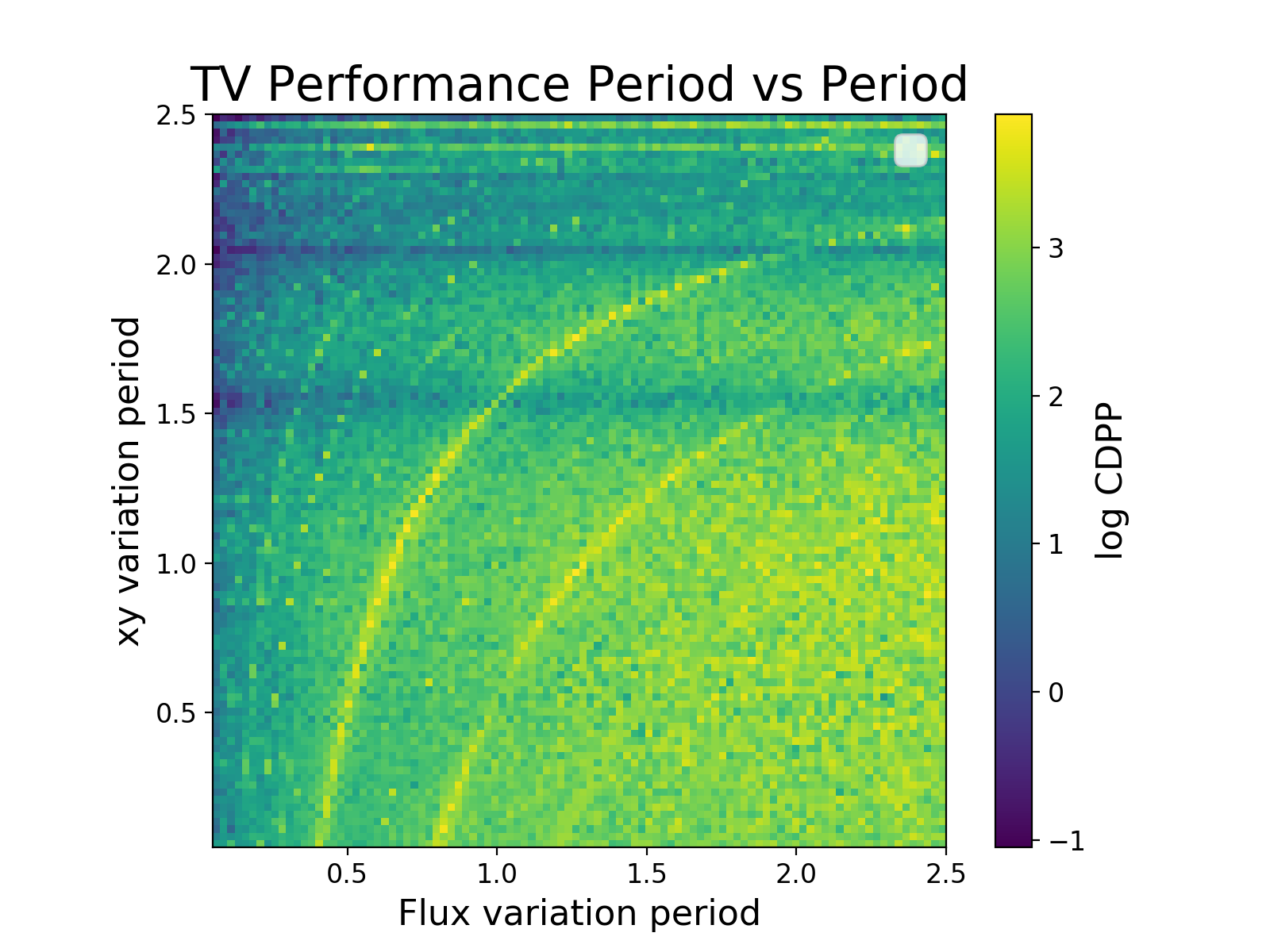
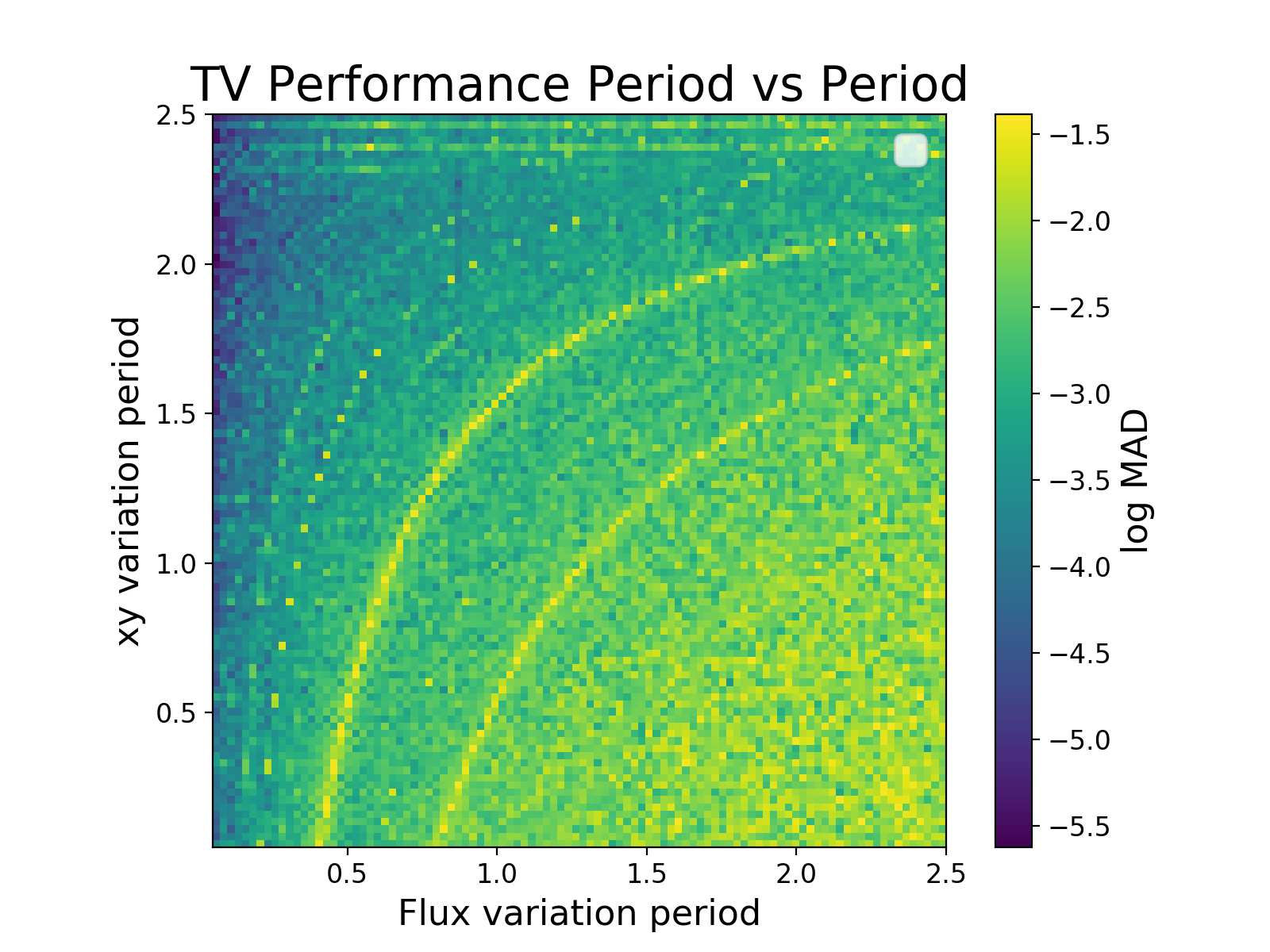
Pleiades

Πλειάδες, the Seven Sisters

Alcyone, Atlas (dad), Electra, Maia, Merope, Taygeta, Pleione (mum)

Atlas lightcurve: raw (top) and halo (bottom)

White, Pope et al., 2017

Lightcurves of All Seven Bright Pleiades

White, Pope et al., 2017

I am currently searching all bright stars in K2 for transiting planets - none so far, but plenty of asteroseismology!

The Future

The method generalizes well to simulated data for the upcoming TESS mission. We have many K2 halo datasets and are working our way through them - between these missions we should cover the whole sky.

We still don't have an explanation for the unreasonable effectiveness of the L1 norm in this algorithm - help us understand!

All our code is open source at github.com/hvidy/halophot - play with it!

We have a solution looking for problems - we want to extend this to TESS, JWST, and even ground-based missions.

We need your help to be able to understand and improve photometry tools.