morphine

Phase Retrieval, Design, and Kernel Phase with Automatic Differentiation

Benjamin Pope, UQ

Slides available at
benjaminpope.github.io/talks/fizeau/fizeau.html

Work in collaboration with Sydney students

Alison Wong (PhD)

and Louis Desdoigts (Honours),

Yinzi Xin (Caltech),

and faculty Peter Tuthill (Sydney)

and Laurent Pueyo (STScI).

Phase Problems in Direct Imaging

The main limitation on direct imaging is from wavefront aberrations which corrupt phase information.

Good and Bad PSFs

Problem 1: Phase Retrieval

Given an image, what were the aberrations in the telescope?

HST Servicing Mission

Problem 2: Phase Design

Given an objective, how do we engineer an optimal PSF?

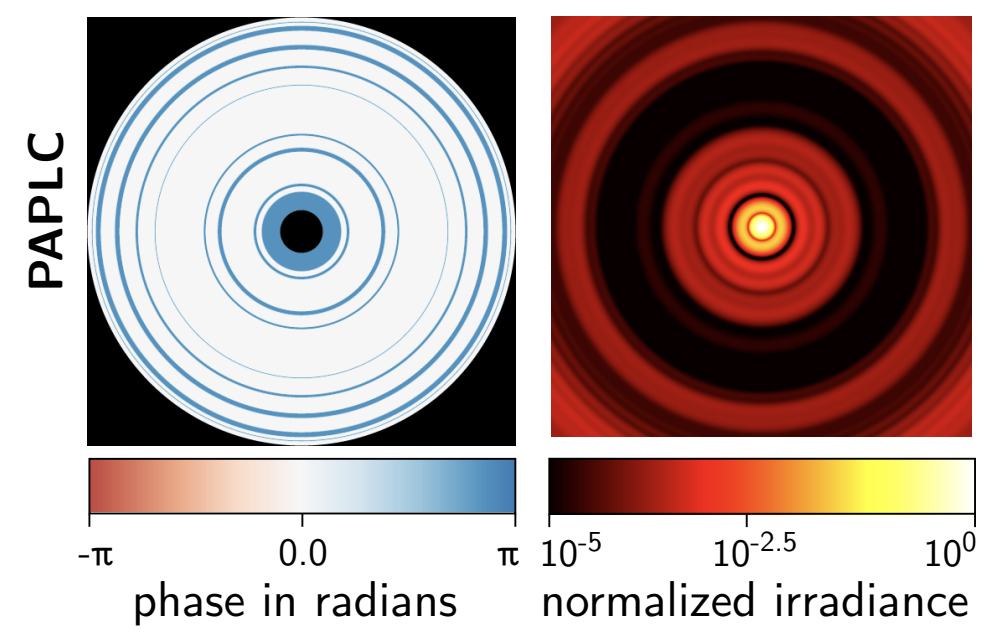
Emiel Por Coronagraph

Phase Apodized Coronagraph: Por, 2019, arXiv:1908.02585

Problem 3: Kernel Phase

How do we correct phase errors in postprocessing?

Automatic Differentiation

So how do we design such complicated optical systems in a principled way?

What if we want to linearize an arbitrary optical system?

Optics is mathematically like machine learning: matrix multiplications and simple nonlinear functions

Can use automatic differentiation!

Autodiff is not finite differences, and it is not symbolic differentiation.

Using the chain rule you can decompose almost-arbitrary code!

Autodiff is the enabling technology for deep neural networks - you use the chain rule to take derivatives of nearly-arbitrary numerical functions.

Implementations in TensorFlow, Theano, PyTorch, Julia...

Here we use Google Jax, which resembles NumPy, to rewrite the Fourier/Fresnel optics code poppy to take derivatives

...Morphine!

Jax permits

Phase Retrieval

Alison Wong - phase retrieval and design by gradient descent

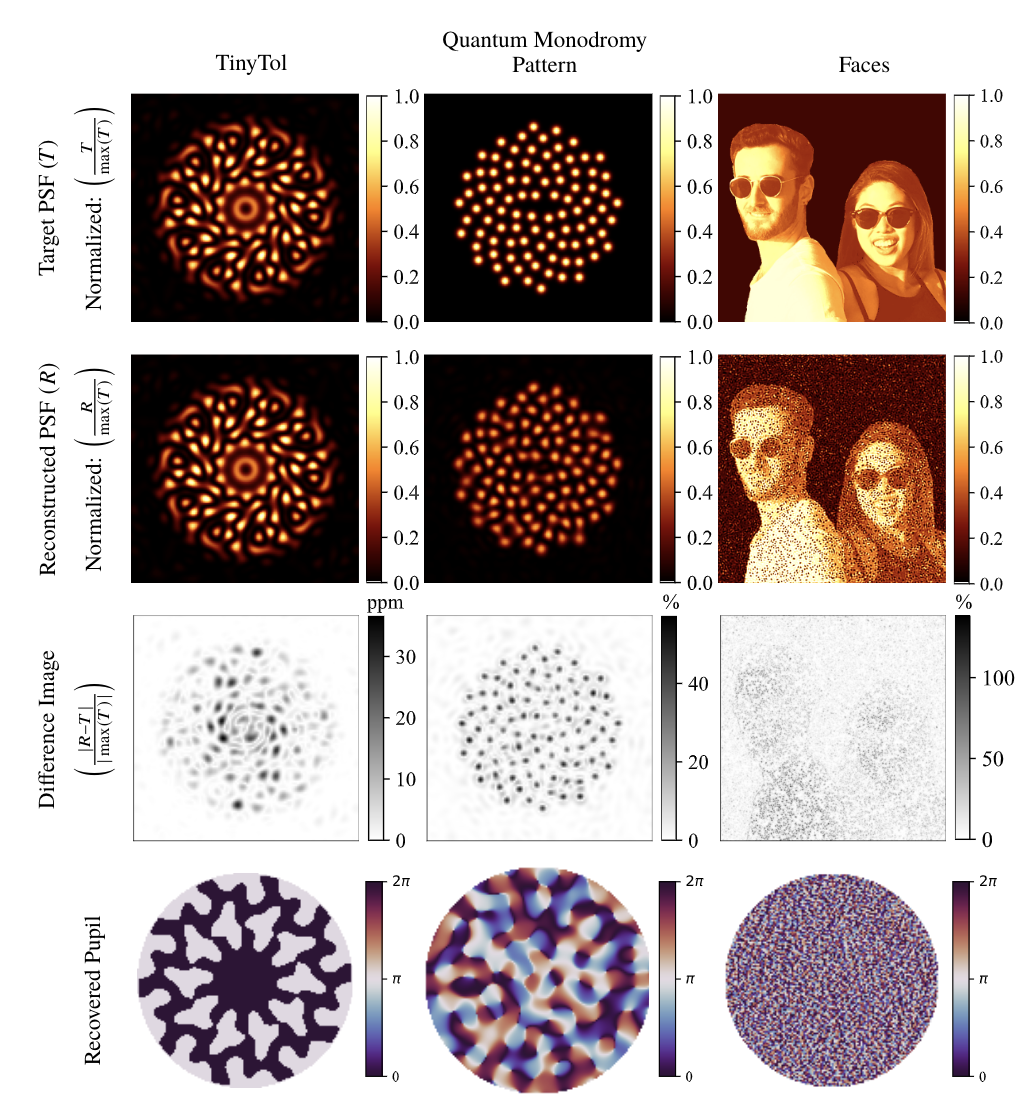
Phase Retrieval
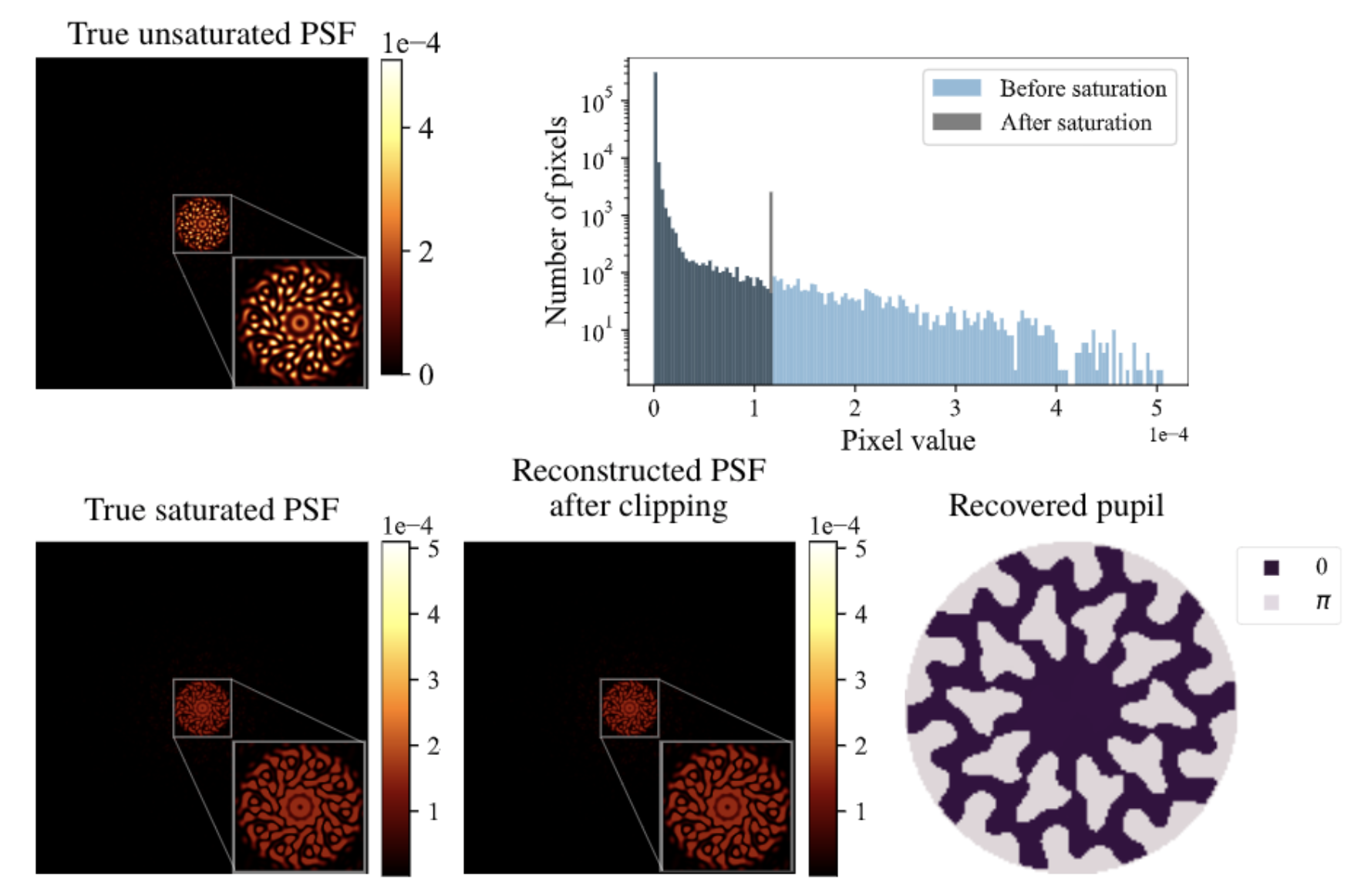
Phase Retrieval with Saturation

Phase Design

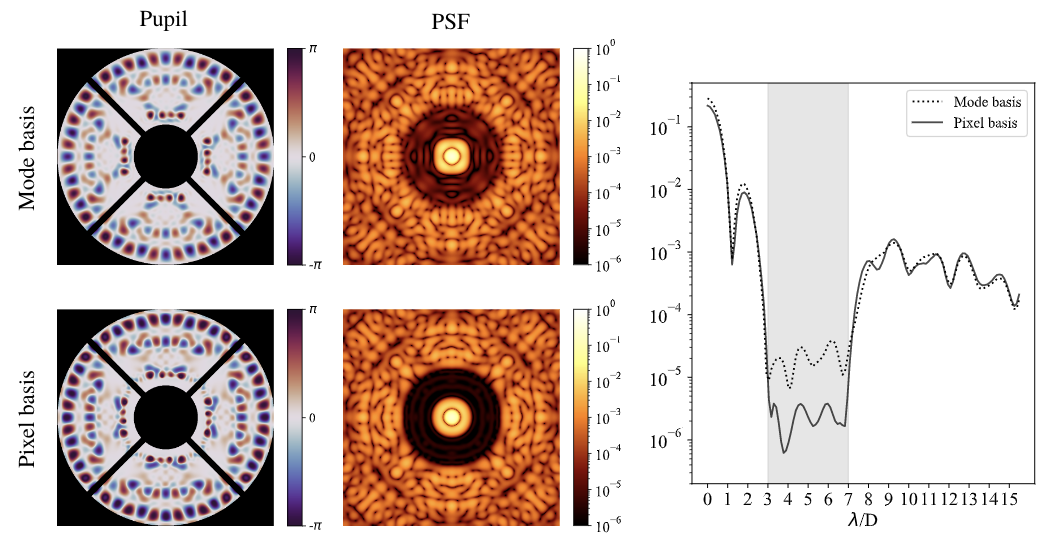
Coronagraph Designs

Coronagraph Phase Mask Design - try it yourself!

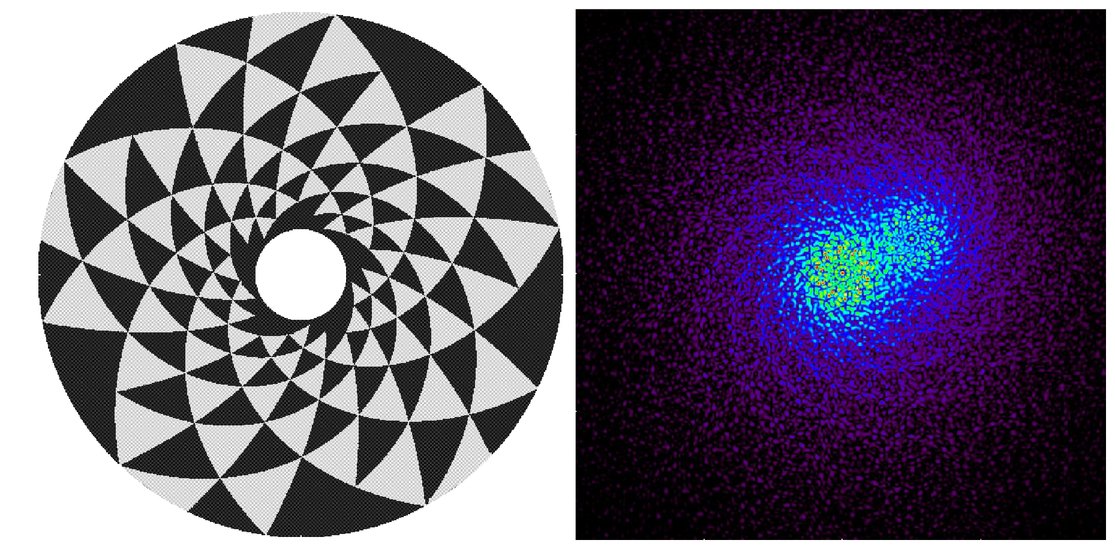
Toliman Mission

Detect planets with μ-arcsec astrometry

Astrometric precision proportional to gradient energy

Use diffractive optic to maximize this subject to constraints

Toliman Pupil and Stars
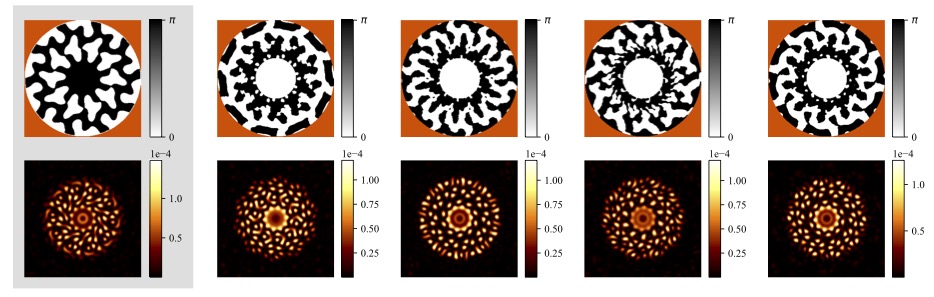
Toliman Designs
Toliman Mask

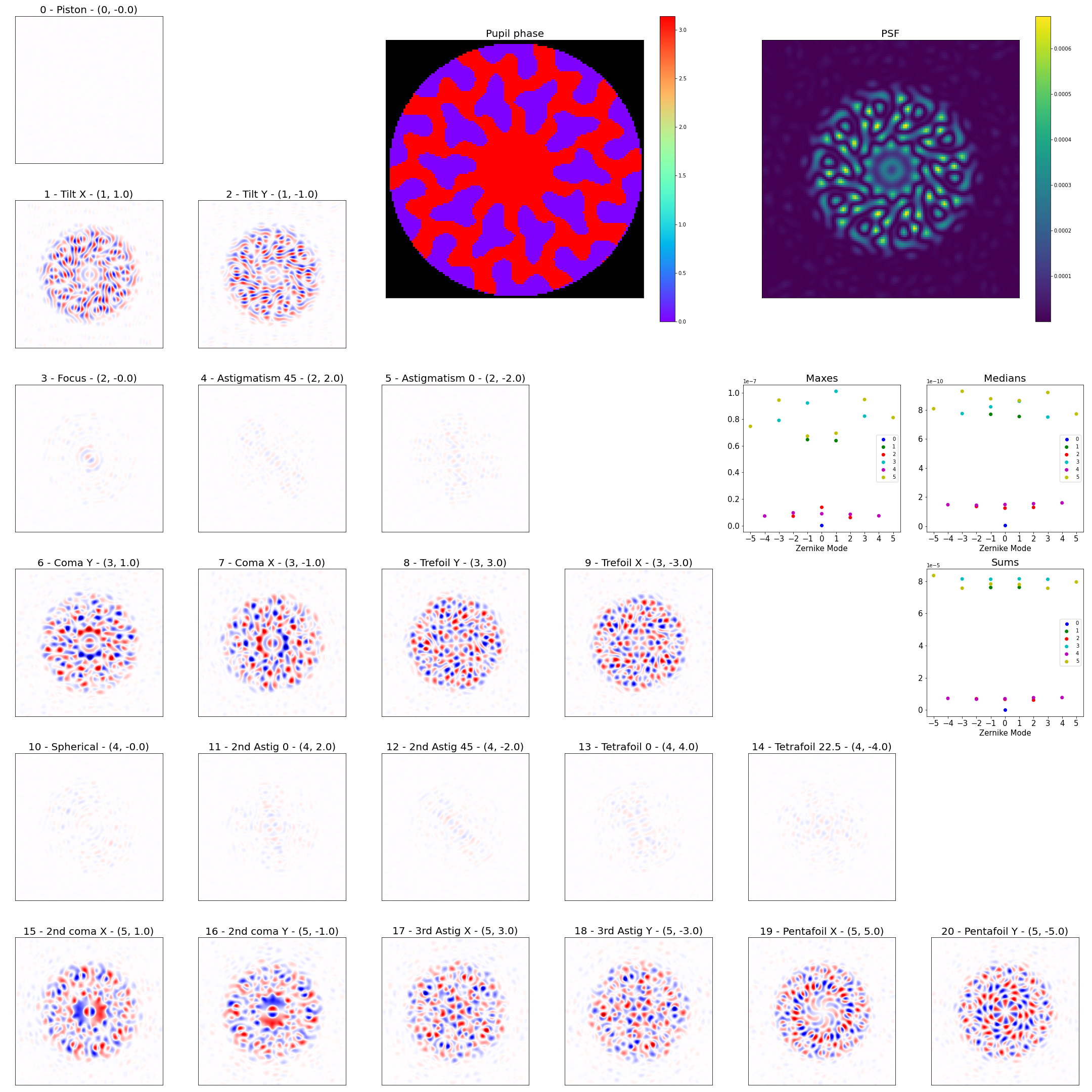
Louis Desdoigts - sensitivity of Toliman to Zernike modes

Toliman Image

Continuous Latent-Image Mask Binarization (CLIMB)

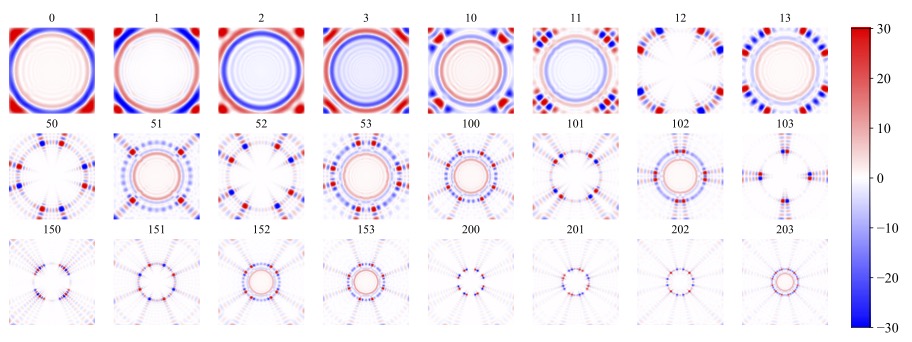
Basis

Basis used in CLIMB

Kernel Phase

In radio astronomy the idea of 'closure phase' was developed to be immune to phase noise:

Correlate baselines around a triangle of receivers

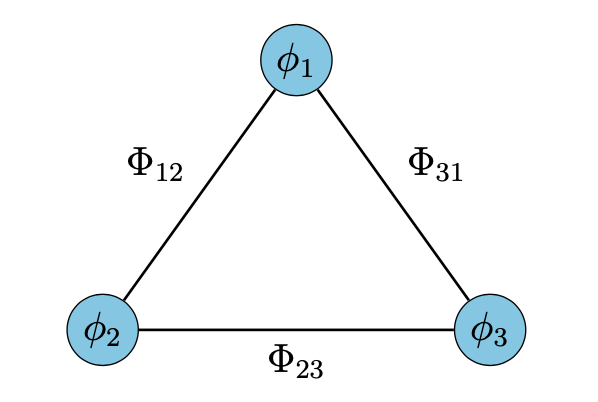
Basis
A baseline phase \(\Phi_{12}\) affected by errors \(\phi_1\) and \(\phi_2\) is observed as \[\Phi'_{12} \equiv \Phi_{12} + \phi_1 - \phi_2. \]
In matrix form, \[\underbrace{\left(\begin{array}{c} \Phi_{12}^\prime\\ \Phi_{23}^\prime\\ \Phi_{31}^\prime \end{array}\right)}_{\text{observed}} = \underbrace{\left(\begin{array}{ccc} 1&-1&0\\ 0&1&-1\\ -1&0&1 \end{array}\right)}_{\text{'transfer matrix' } \mathbf{A}_\phi} \cdot \underbrace{\left(\begin{array}{c} \phi_1\\ \phi_2\\ \phi_3 \end{array}\right)}_\text{noise} + \underbrace{\left(\begin{array}{c} \Phi_{12}\\ \Phi_{23}\\ \Phi_{31} \end{array}\right)}_\text{true} \]
The closure phase operator \[C_\phi \equiv \left(\begin{array}{ccc} 1&1&1 \end{array}\right) \] annihilates this matrix as \(C_\phi \cdot \mathbf{A}_\phi = \mathbf{0}\), leaving zero phase error!

Kernel phase is a generalization of closure phase to arbitrary pupils.

Take the SVD of a phase error transfer matrix - separate into good and bad observables

Linearize response to phase noise - need derivative

Jacobian matrix is gradient of vector function \(\mathbf{y}(\mathbf{\theta})\):

\[ J_{i,j} \equiv \frac{\partial{y_i}}{\partial{\theta_j}} \\ \]

The Martinache 2010 phase transfer matrix \(\mathbf{A}_\phi\) is an analytically determined Jacobian, mapping pupil phases to their u, v effects.

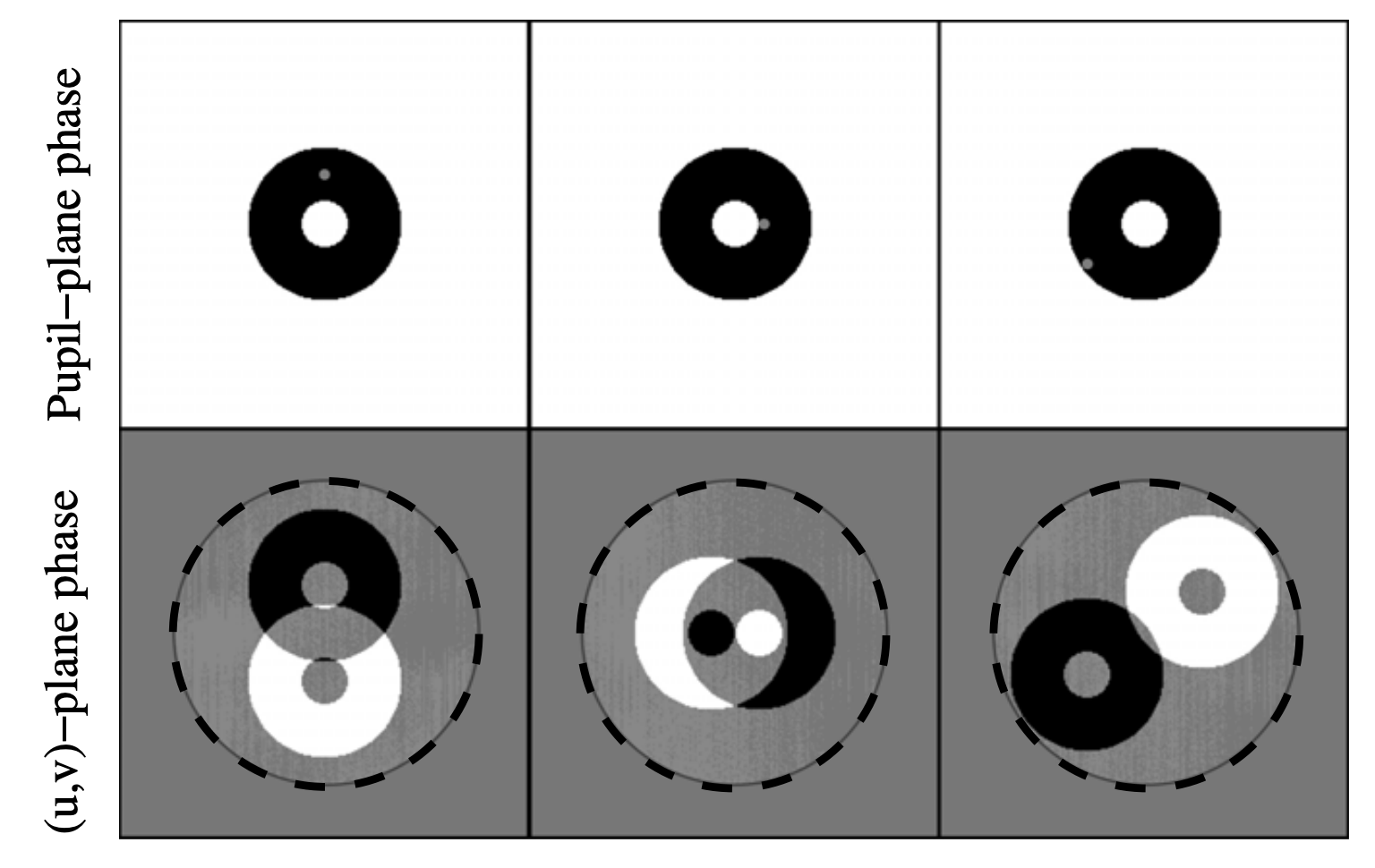
Martinache, 2010
How do we use autodiff to generalize kernel phase?

Check out this notebook!

The Future

Get using morphine and read the paper!

What else can we use this for?

Questions!