How to Find an Exoplanet

(with Gaussian Processes)

Benjamin Pope

Slides available at
benjaminpope.github.io/talks/capstone/capstone.html QR Code

Transiting Planets

Exoplanet-style transit light curve of Venus from James Gilbert on Vimeo.

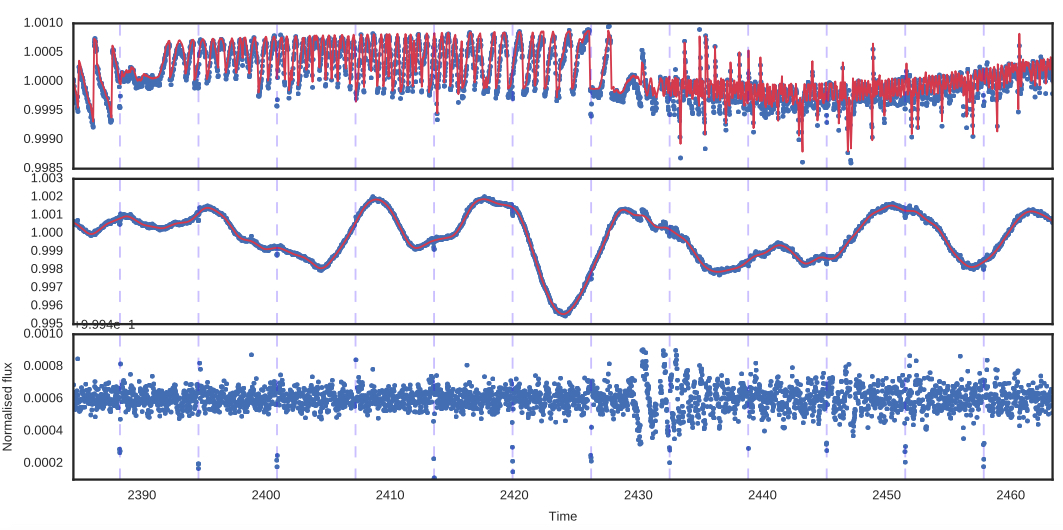
Kepler Photometry

The Kepler Space Telescope, launched in 2009, looks for planets by the transit method, and also does asteroseismology.
After the failure of a reaction wheel in 2012, it is now operating as the 'K2 Mission', with very unstable pointing (hence the shaking in the videos you'll see).
To get the photometry, you can just sum the pixel values in a window containing the whole PSF...

but the pixels have different gains ("inter- and intra-pixel sensitivity variation")...

and the pixel window doesn't necessarily track the whole PSF perfectly ("aperture losses").

In our group's pipeline we use Gaussian Process models to detrend the flux time series with respect to the position of the star.

By subtracting the GP time and spatial components, we can find a transiting planet!

K2SC Figure 2
So what are Gaussian Processes?
For a great overview, see Roberts et al, 2012, "Gaussian Processes for Timeseries Modelling" (tinyurl.com/wohyqvj)

Also see Dan Foreman-Mackey's tutorial, An Astronomer's Introduction to Gaussian Processes (tinyurl.com/swbgsmd)

Or David Mackay's free book Information Theory, Inference, and Learning Algorithms (tinyurl.com/yxeyve76)

Or the great book, Rasmussen & Williams (gaussianprocess.org).

Gaussian processes are a method of non-parametric inference.

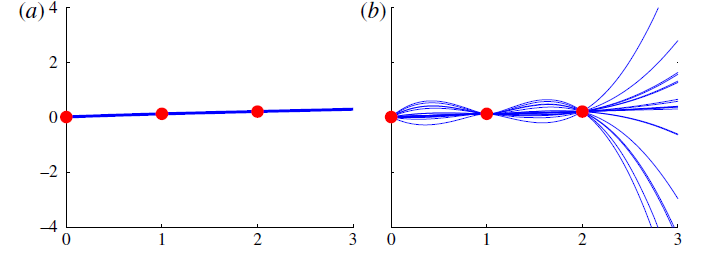
GPs provide a pdf over functions

You can use these to fit to variations in time series, spectroscopic, spatial data... whatever you want

Splines are okay for non-parametric fitting...

but they can blow up unrealistically.

Splines Figure

Roberts et al 2012

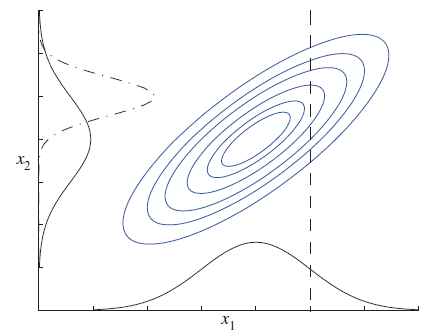
Consider a correlated Gaussian in 2D Correlated Gaussian

Roberts et al 2012

Knowing the value of \(x_1\) constrains the value of \(x_2\)

This information is contained in the covariance matrix

\[K = \begin{bmatrix} \sigma_1 & \kappa\\ \kappa&\sigma_2 \end{bmatrix}\]

How do we generalize this to higher dimensions?

In a GP you consider \(n\) points drawn from a multidimensional Gaussian

\[p(\mathbf{y}(\mathbf{x})) \sim \mathscr{N}(\mathbf{\mu}(\mathbf{x}),K(\mathbf{x},\mathbf{x}))\]

with covariance

\[K(\mathbf{x},\mathbf{x}) = \begin{bmatrix} k(x_1,x_1) & k(x_1,x_2) & ... & k(x_1,x_n) \\ k(x_2,x_1) & k(x_2,x_2) & ... & k(x_2,x_n) \\ \vdots &\vdots &\vdots &\vdots \\ k(x_n,x_1) & k(x_n,x_2) & ... & k(x_n,x_n) \end{bmatrix}\]

A common kernel is the squared exponential kernel:

\[k(x_i,x_j) = h^2 \exp({-(\frac{x_i - x_j}{\lambda})^2})\]

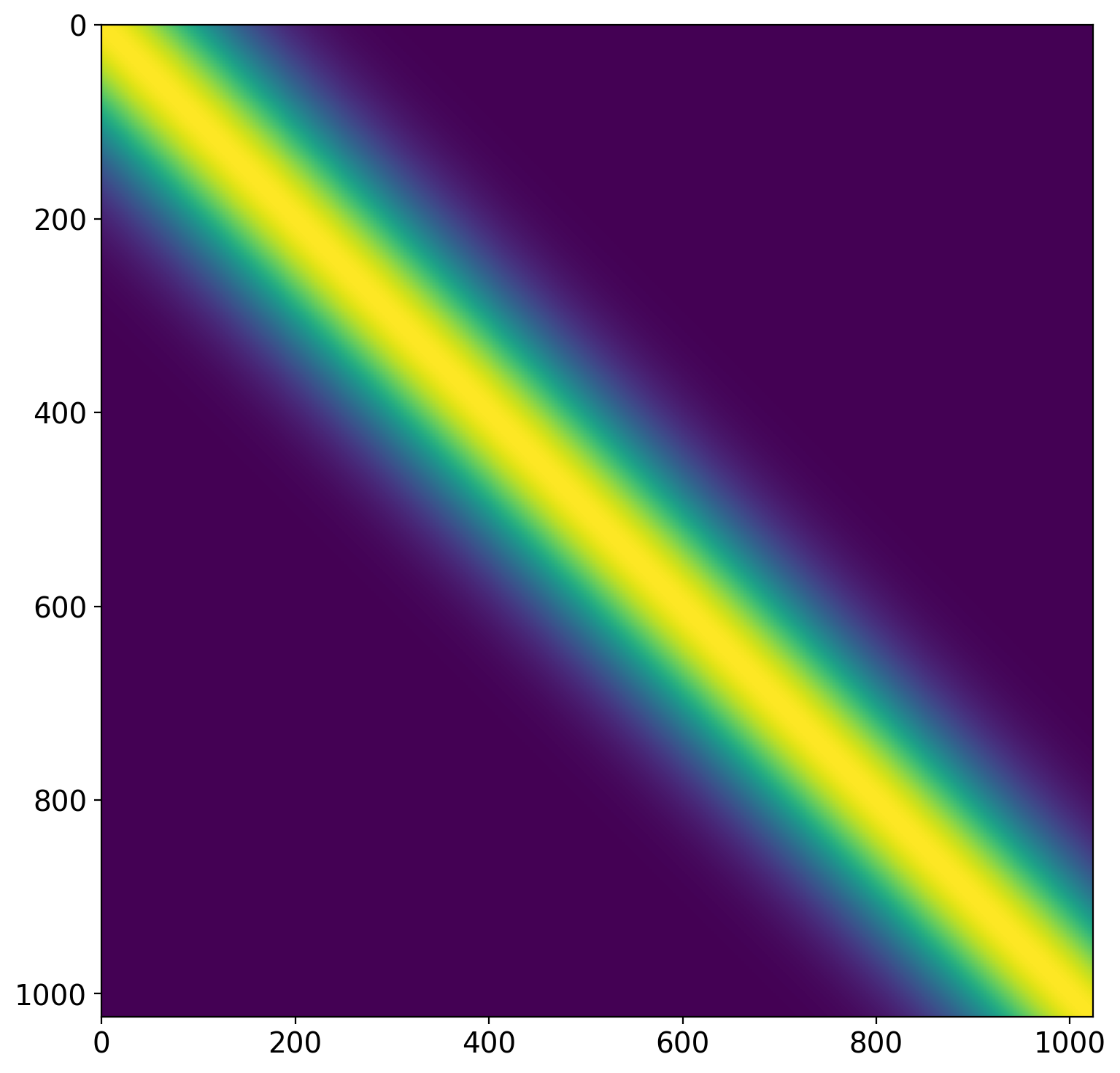
Squared Exponential kernel
Alternatively, an exponential sine-squared kernel:

\[k(x_i,x_j) = h^2 \exp(-\Gamma {\sin^2}[\frac{\Pi}{P} |x_i - x_j|]) \]

Periodic Kernel
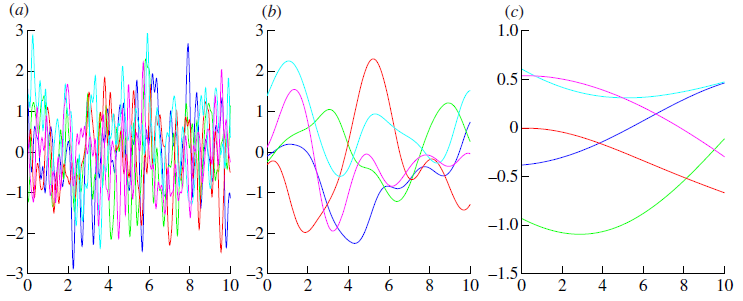
Draws from GPs with vertical scale \(h=1\) and horizontal correlation length \(\lambda\) a) 0.1, b) 1, c) 10 Draws

Roberts et al 2012

In practice:
  • Write down a kernel
  • Optimize hyperparameters with respect to data
  • Calculate the posterior mean
Careful - scales as \( \mathscr{O}(N^3) \)!

(except in special cases)

Applying a GP to real data

Follow along in a Google Colab online:
tinyurl.com/t5j2ncs
QR Code