Finding Transiting Exoplanets

The Data Challenge

Benjamin Pope, NYU

Slides available at
benjaminpope.github.io/talks/ranganath/ranganath.html

Transiting Planets

Exoplanet-style transit light curve of Venus from James Gilbert on Vimeo.

Large searches for exoplanets like the Kepler mission have shown planets to be common in our Galaxy - now we want to learn about their atmospheres and compositions.

The best options are those around bright stars, like 55 Cancri e - subject of 367 papers in the last decade!

My Sagan Fellowship project is to search for planets transiting naked-eye stars (V mag < 6.5) in order to find ideal targets for characterization with the upcoming James Webb Space Telescope.

Kepler Photometry

The Kepler Space Telescope, launched in 2009, looks for planets by the transit method, and also does asteroseismology.
After the failure of a reaction wheel in 2012, it is now operating as the 'K2 Mission', with very unstable pointing (hence the shaking in the videos you'll see).
To get the photometry, you can just sum the pixel values in a window containing the whole PSF...

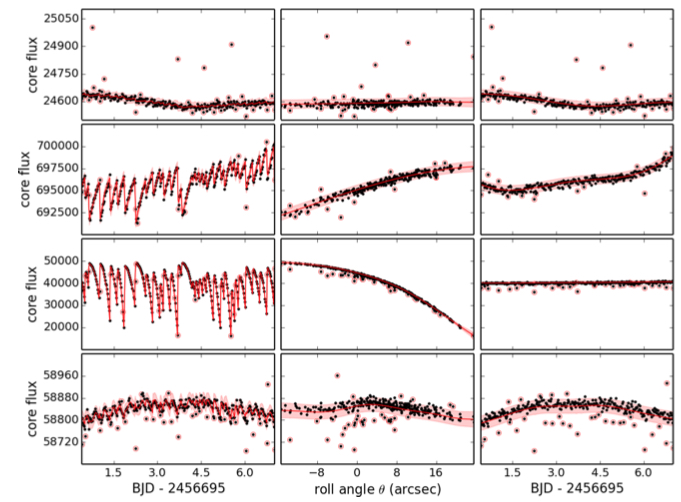
but the pixels have different gains ("inter- and intra-pixel sensitivity variation")...

and the pixel window doesn't necessarily track the whole PSF perfectly ("aperture losses").

In our group's pipeline we use Gaussian Process models to detrend the flux time series with respect to the position of the star.

Raw - GP in position - GP in time

K2SC Figure

By subtracting the GP time and spatial components, we can find a transiting planet!

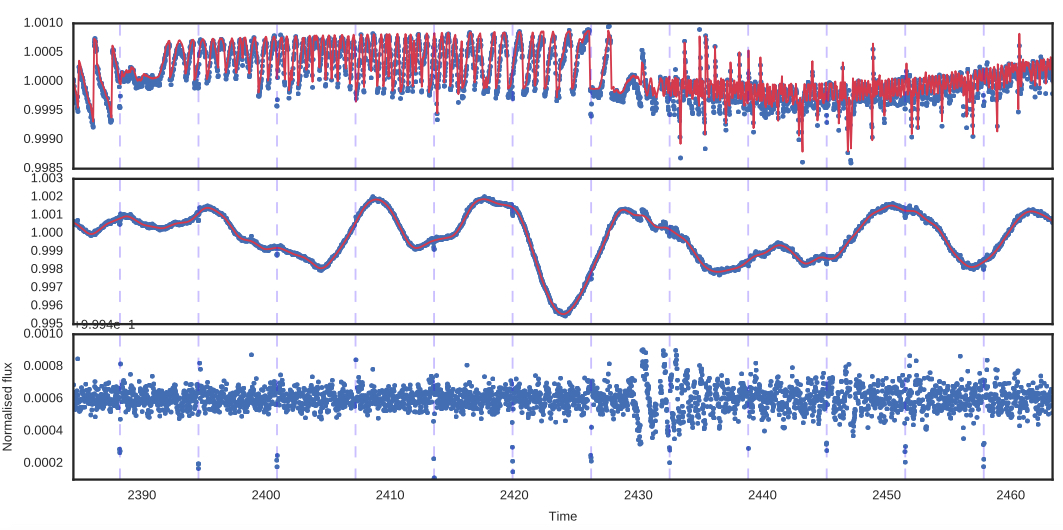
K2SC Figure 2
Alternatively, the EVEREST model (Luger et al, 2016) does 'pixel-level decorrelation', fitting a linear combination of pixel time series to the data, getting excellent photometry.

We will be motivated by this here.

For sufficiently bright stars, though, light fills the CCD wells with electrons that spill up and down the column, ruining the photometry as they leave the aperture.
Kepler saturates on stars brighter than ~ 11th mag (log scale: 5 mag = factor of 100) - but we want to look at stars 10k times brighter.

Halo Photometry

What if we just look at unsaturated pixels?
Flux \(f_i \) at cadence i is a sum over j pixels \(p_{ij}\) with weights \(w_j\):

\[ f_i \equiv \sum\limits_i w_j p_{ij} \]
In the OWL method (Hogg & Foreman-Mackey), you choose weights to minimize variance of the final light curve - but this has limited success.
To find the appropriate weights, we instead started by minimizing the Total Variation

\[\begin{align} TV \equiv \sum_i |f_i - f_{i-1}| \end{align} \] subject to constraints \[\begin{align}\forall_j w_j &> 0\\ \sum_{i=1}^{N} f_i &= N.\end{align} \]

This is the \(L_1\) norm or 'taxicab metric' on the derivative of the time series.

This has analytic derivatives you can compute with autograd - easy to optimize.

We have recently improved this by minimizing the lagged Total Variation

\[\begin{align} TV_δ \equiv \sum_i |f_{i} - f_{i-δ}| \end{align} \]

We can also generalize the \(L_1\) norm to the \(L_k\) norm \[Q_{k,\delta} \equiv {\sum_i{|f_i - f_{i-\delta}|^k}}\]

This has analytic derivatives you can compute with e.g. autograd - easy to optimize.

Note that these light curves are basically a sum of sine waves - anything but sparse in the derivative!

But they're sparse in the Fourier domain... perhaps this is relevant?

All K2 Halo data are available online at github.com/benjaminpope/k2halo

The Future

The method generalizes well to simulated data for the upcoming TESS mission. We have many K2 halo datasets and are working our way through them - between these missions we should cover the whole sky.
We still don't have an explanation for the unreasonable effectiveness of the L1 norm in this algorithm - help us understand!
All our code is open source at github.com/hvidy/halophot - play with it!
We have a solution looking for problems - we want to extend this to TESS, JWST, and even ground-based missions.

We need your help to be able to understand and improve photometry tools.