Swinburne Colloquium Seminar: Benjamin Pope

All Downhill from Here

What Automatic Differentiation can Do for Optics

Benjamin Pope, UQ

Slides available at
benjaminpope.github.io/talks/swinburne/swinburne.html

Work in collaboration with Sydney students

Alison Wong and Louis Desdoigts,

and faculty Peter Tuthill (Sydney)

and Laurent Pueyo (STScI).

Direct Imaging

We are starting to detect planets at the epoch of formation - eg the accreting protoplanets PDS 70 bc.

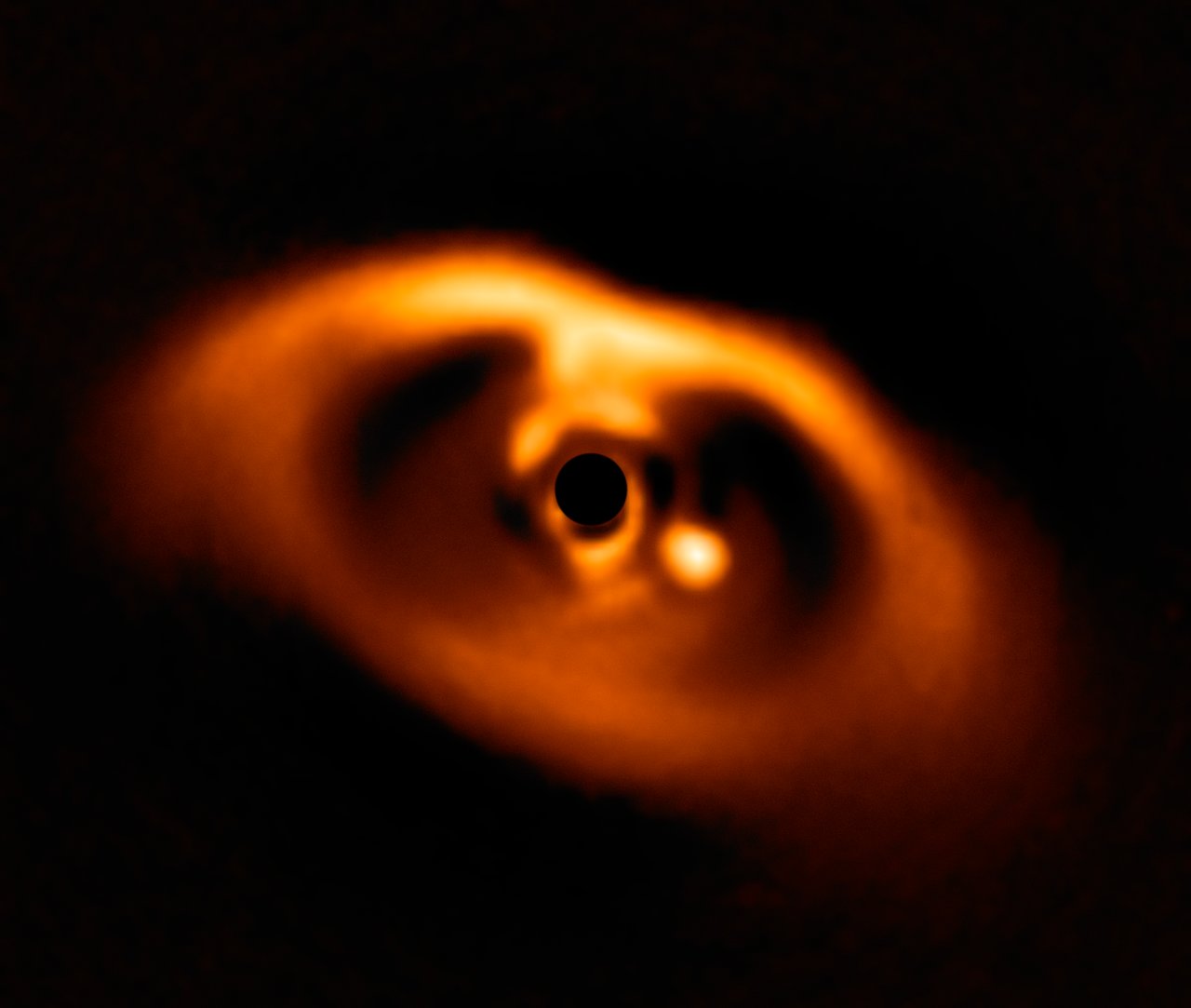
(ESO/A. Müller et al.)

Candidate around our nearest neighbour, α Cen!

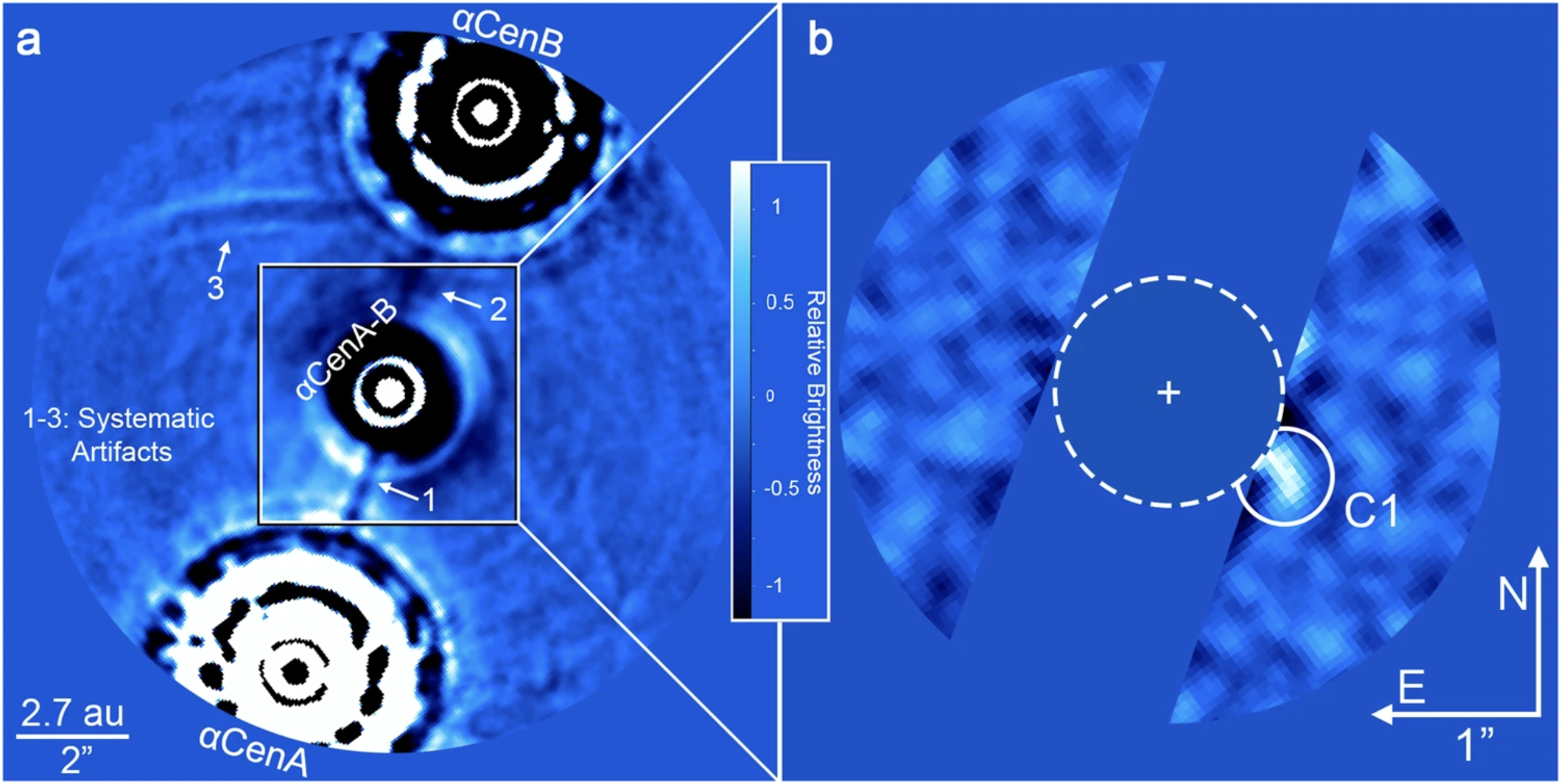
(Wagner et al., 2021)

Coronagraphs

Lyot Coronagraph - Credit: Rebecca Oppenheimer, Lyot Project

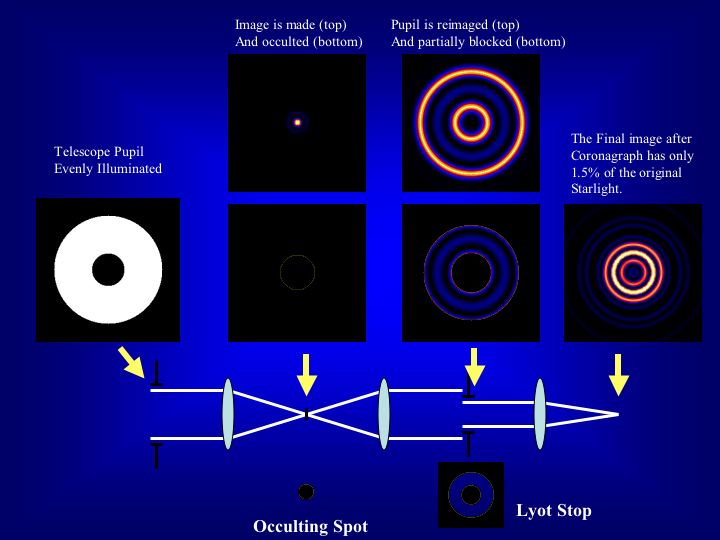
Credit: Rebecca Oppenheimer, Lyot Project

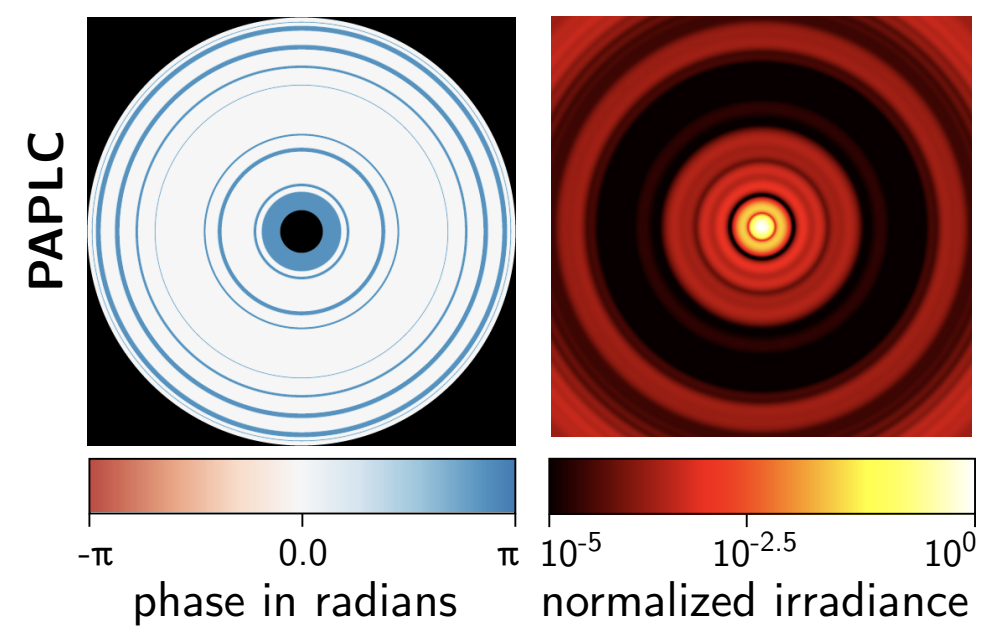
Phase Apodized Coronagraph: Por, 2019, arXiv:1908.02585

Toliman Space Telescope

Book of Fixed Stars,
'Abd al-Rahman al-Sufi,
MS. Marsh 144,
Bodleian Library

rijl qanturis

which is the one drawn
on the southern astrolabe

Detect planets with μ-arcsec astrometry

Astrometric precision proportional to gradient energy

Use diffractive optic to maximize this subject to constraints

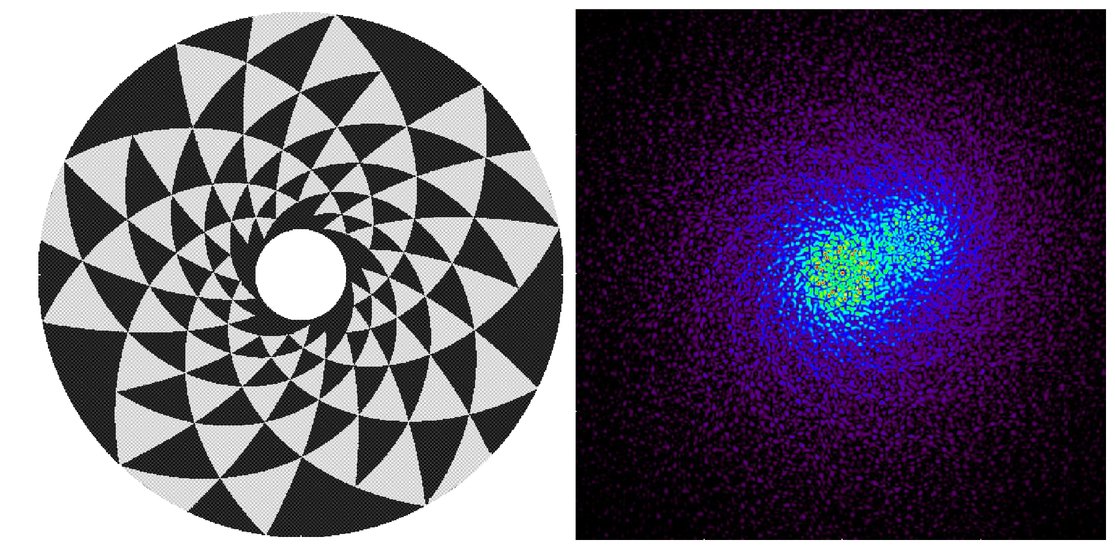
Early pupil design & simulation

TOLIMAN lab test phase mask

Phase Problems in Direct Imaging

The main limitation on direct imaging is from wavefront aberrations which corrupt phase information.

Problem 1: Phase Retrieval

Given an image, what were the aberrations in the telescope?

Problem 2: Phase Design

Given an objective, how do we engineer an optimal PSF?

Phase Apodized Coronagraph: Por, 2019, arXiv:1908.02585

Problem 3: Kernel Phase

How do we correct phase errors in postprocessing?

See our paper: arXiv:2011.09780!

Automatic Differentiation

So how do we design such complicated optical systems in a principled way?

What if we want to linearize an arbitrary optical system?

Optics is mathematically like machine learning: matrix multiplications and simple nonlinear functions

Can use automatic differentiation!

Autodiff is not finite differences, and it is not symbolic differentiation.

Using the chain rule you can decompose almost-arbitrary code!

Autodiff is the enabling technology for deep neural networks - you use the chain rule to take derivatives of nearly-arbitrary numerical functions.

Implementations in TensorFlow, Theano, PyTorch, Julia...

Here we use Google Jax, which resembles NumPy, to rewrite the Fourier/Fresnel optics code poppy to take derivatives

...Morphine!

Jax permits

Just-in-time 'jit' compilation - so faster than normal poppy.
Accelerated Linear Algebra (XLA) - including on GPUs
Automatic differentiation!

Phase Retrieval

Alison Wong - phase retrieval and design by gradient descent

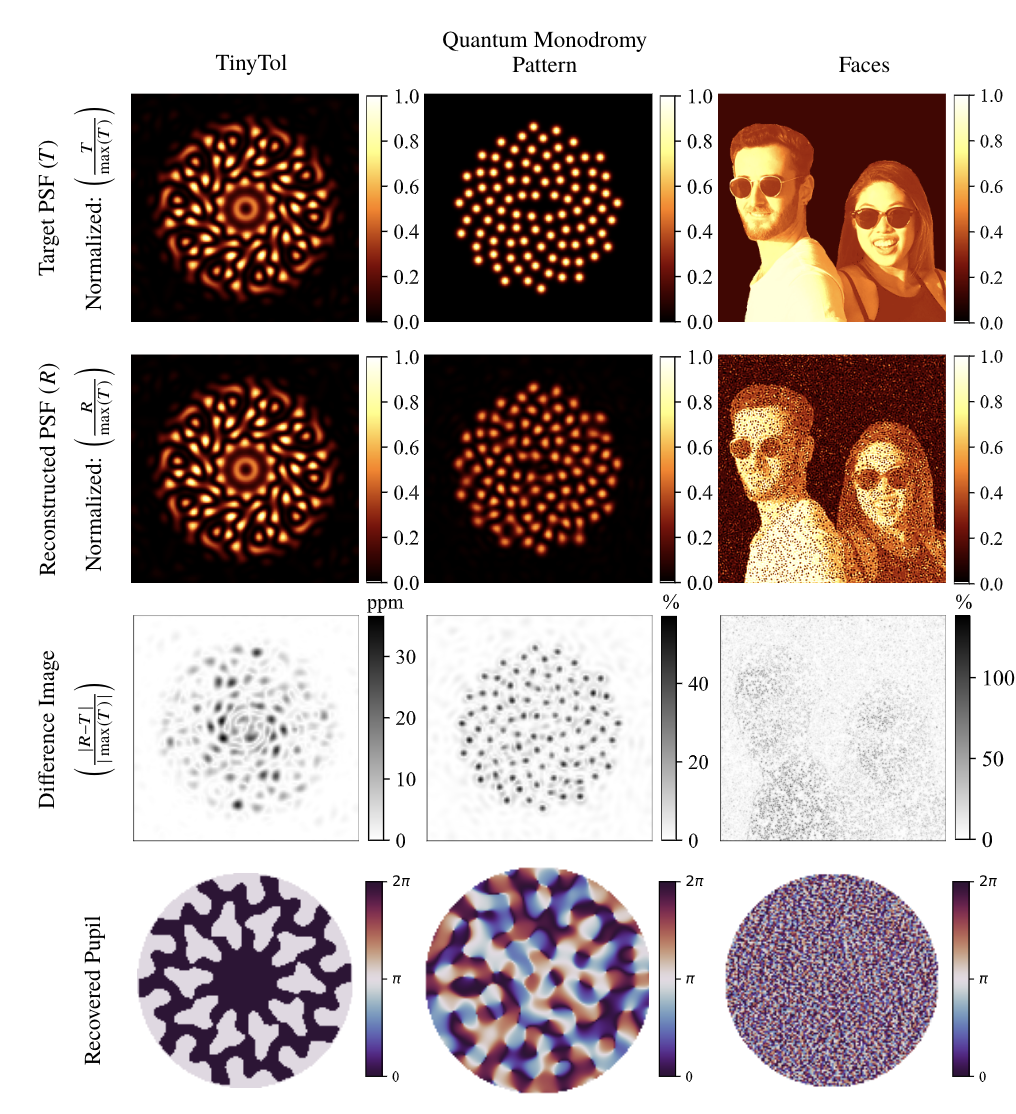
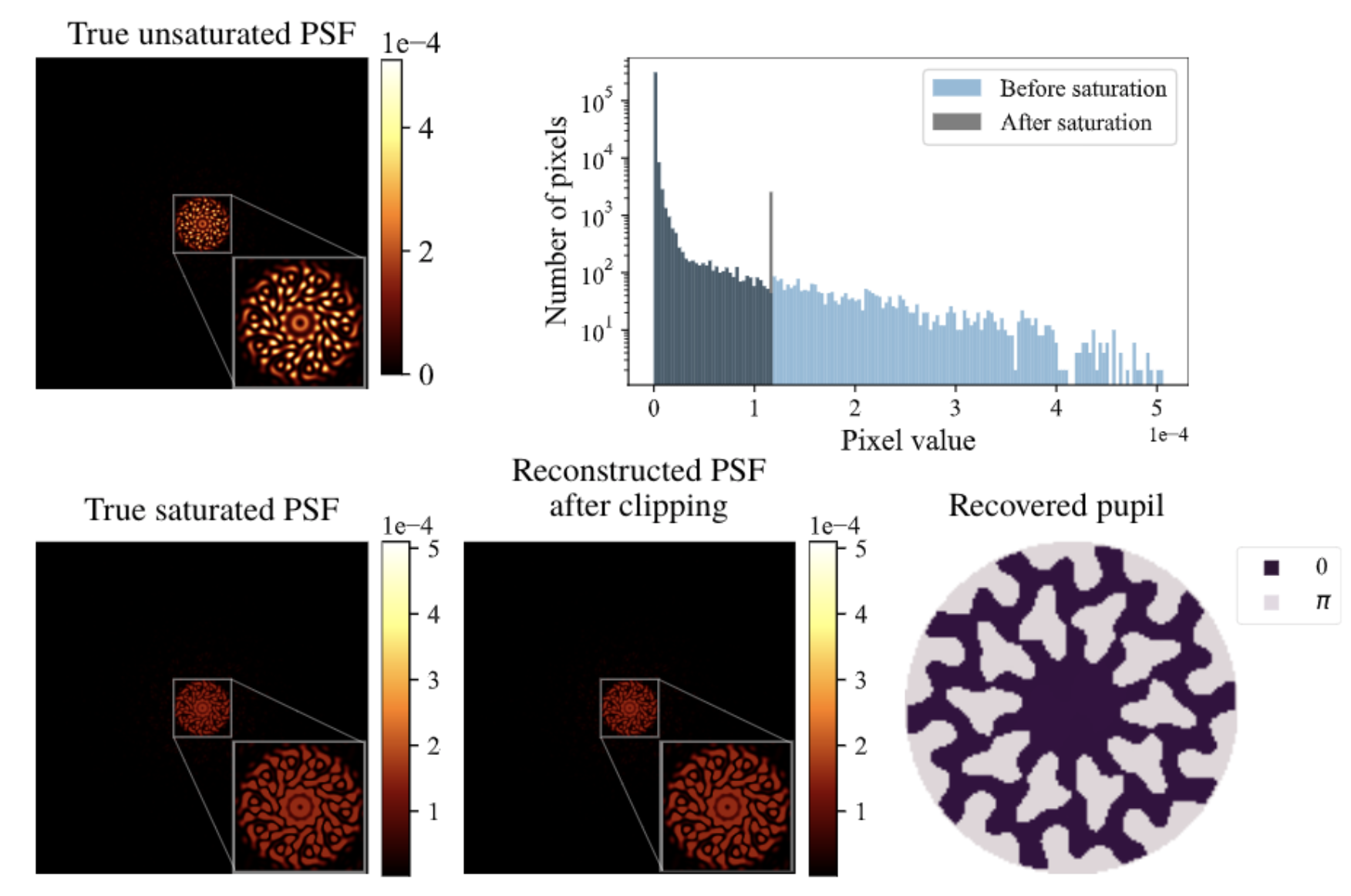
Phase Design

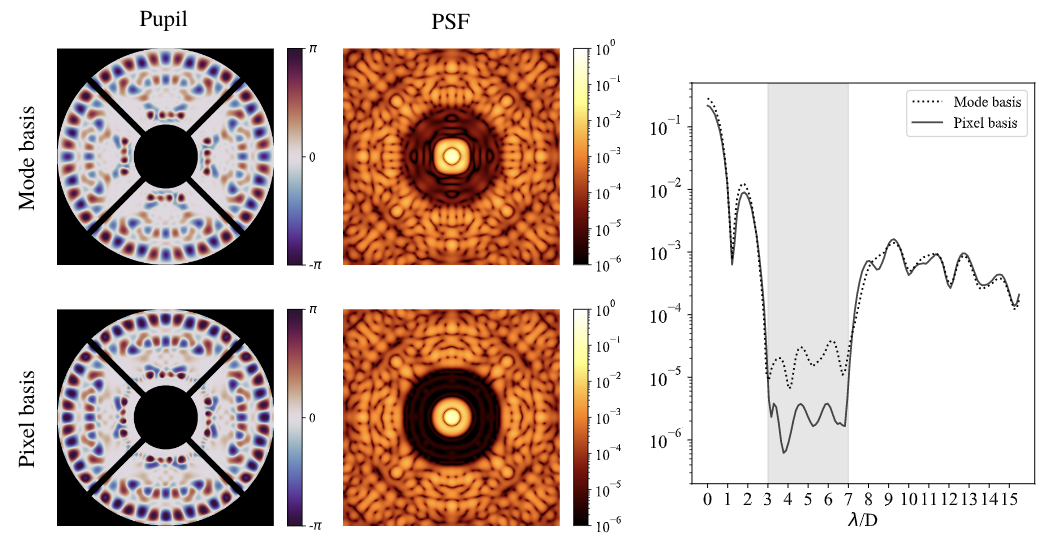
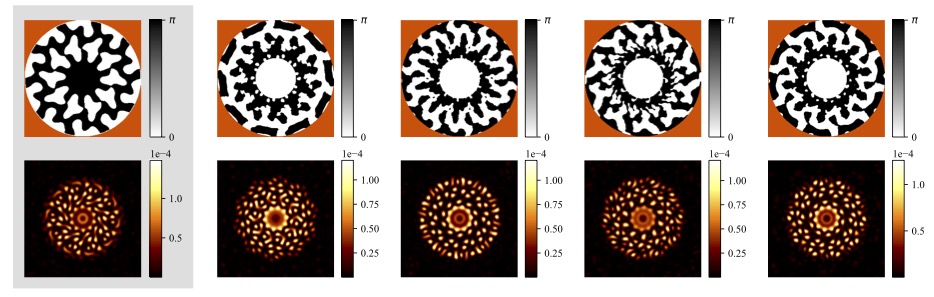
Coronagraph Phase Mask Design - try it yourself!

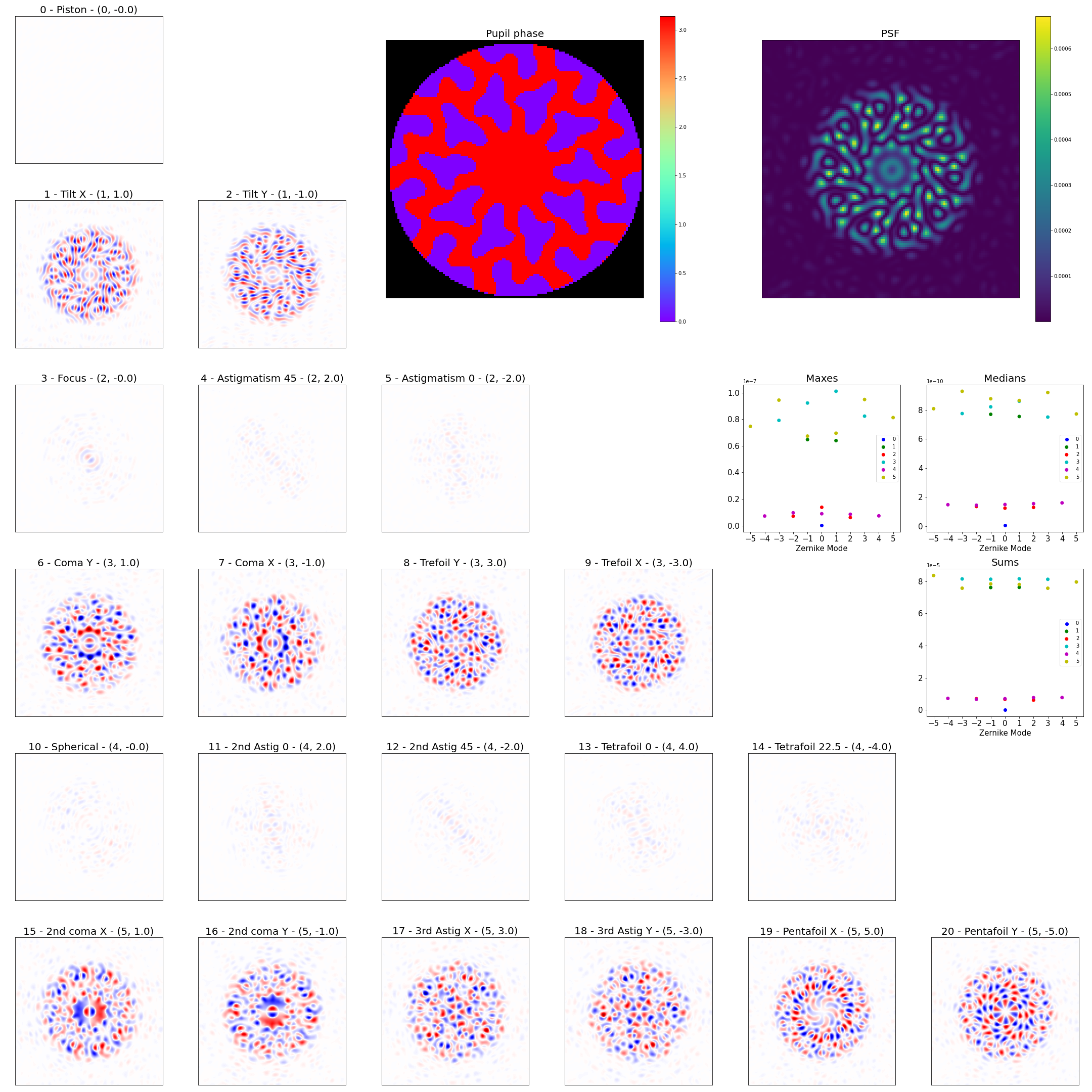
Louis Desdoigts - sensitivity of Toliman to Zernike modes

Continuous Latent-Image Mask Binarization (CLIMB)

Kernel Phase

In radio astronomy the idea of 'closure phase' was developed to be immune to phase noise:

Correlate baselines around a triangle of receivers

JWST has an aperture masking instrument on NIRISS to obtain closure phases

A baseline phase \(\Phi_{12}\) affected by errors \(\phi_1\) and \(\phi_2\) is observed as \[\Phi'_{12} \equiv \Phi_{12} + \phi_1 - \phi_2. \]

In matrix form, \[\underbrace{\left(\begin{array}{c} \Phi_{12}^\prime\\ \Phi_{23}^\prime\\ \Phi_{31}^\prime \end{array}\right)}_{\text{observed}} = \underbrace{\left(\begin{array}{ccc} 1&-1&0\\ 0&1&-1\\ -1&0&1 \end{array}\right)}_{\text{'transfer matrix' } \mathbf{A}_\phi} \cdot \underbrace{\left(\begin{array}{c} \phi_1\\ \phi_2\\ \phi_3 \end{array}\right)}_\text{noise} + \underbrace{\left(\begin{array}{c} \Phi_{12}\\ \Phi_{23}\\ \Phi_{31} \end{array}\right)}_\text{true} \]

The closure phase operator \[C_\phi \equiv \left(\begin{array}{ccc} 1&1&1 \end{array}\right) \] annihilates this matrix as \(C_\phi \cdot \mathbf{A}_\phi = \mathbf{0}\), leaving zero phase error!

Kernel phase is a generalization of closure phase to arbitrary pupils.

Linearize response to phase noise: suitable for stable high Strehl images, with point-source calibrators

Separate out linear subspaces of Fourier components that are immune to phase noise vs susceptible

Linearize response to phase noise - need derivative

Jacobian matrix is gradient of vector function \(\mathbf{y}(\mathbf{\theta})\):

\[ J_{i,j} \equiv \frac{\partial{y_i}}{\partial{\theta_j}} \\ \]

Used this in Pope et al, 2013 to revisit the Reid et al 2006, 2008 HST NICMOS volume-limited brown dwarf surveys and discover 5 additional tight binaries.

The other subspace can be used for wavefront sensing

Every point source image gives you a free wavefront measurement in the instrument pupil!

Cophasing segmented mirror in the lab (Pope+2014)

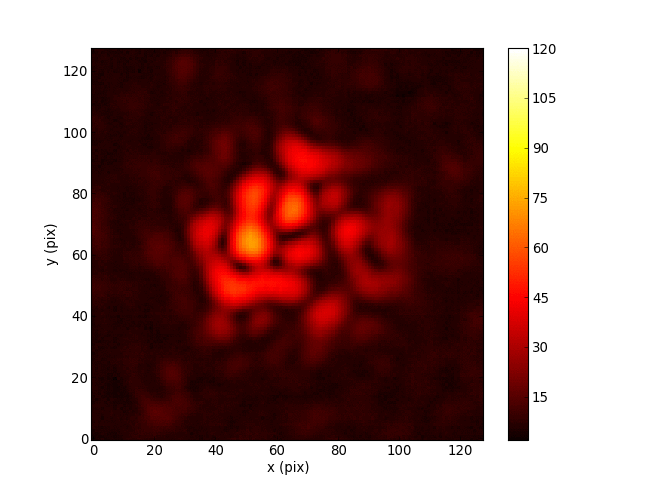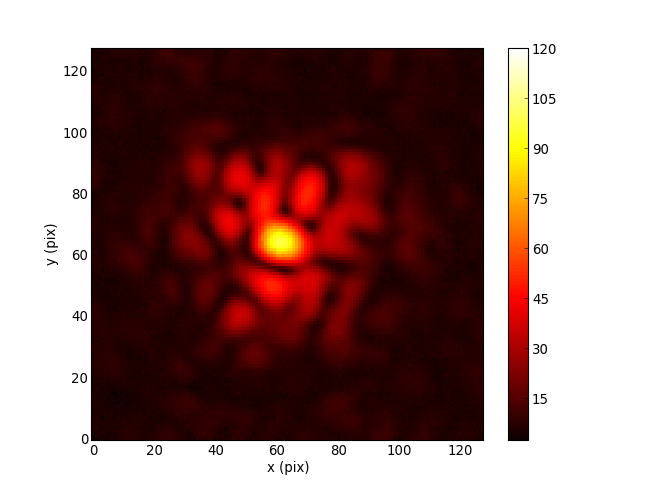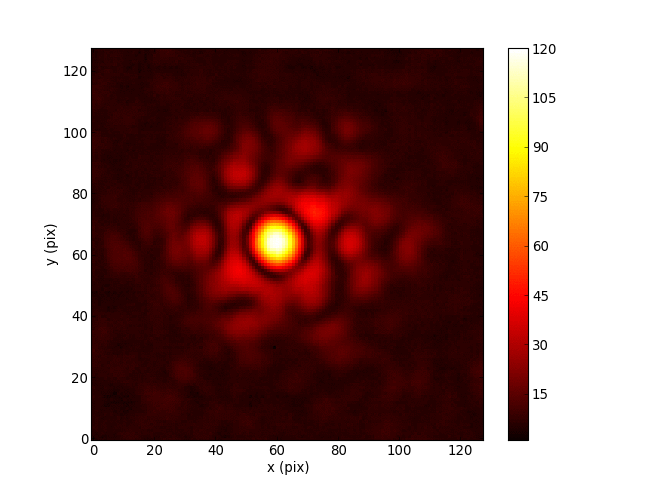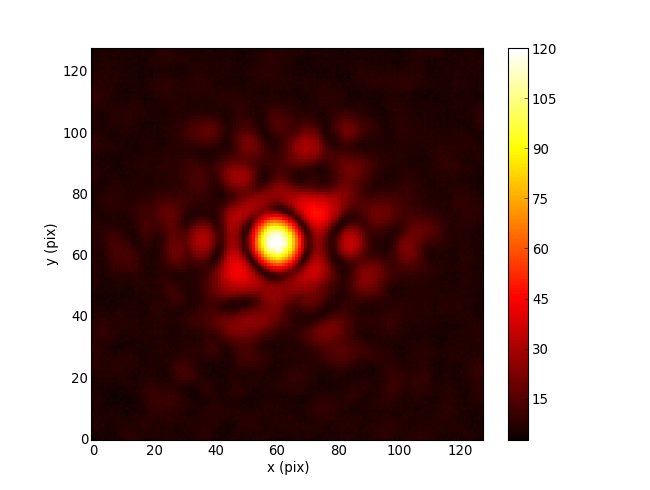
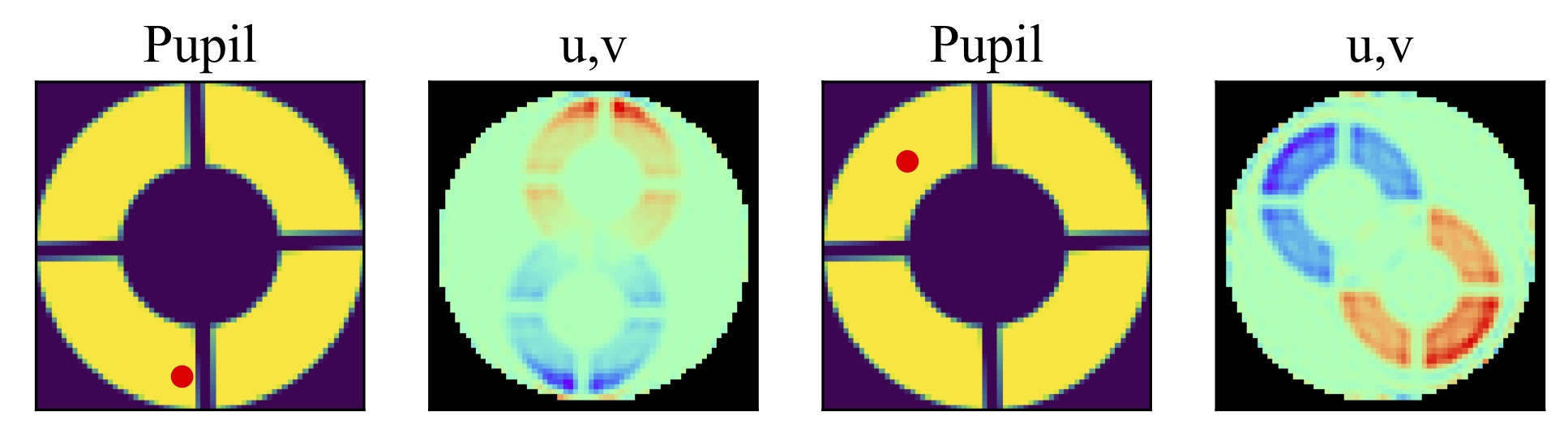
The Martinache 2010 phase transfer matrix \(\mathbf{A}_\phi\) is an analytically determined Jacobian, mapping pupil phases to their u, v effects.

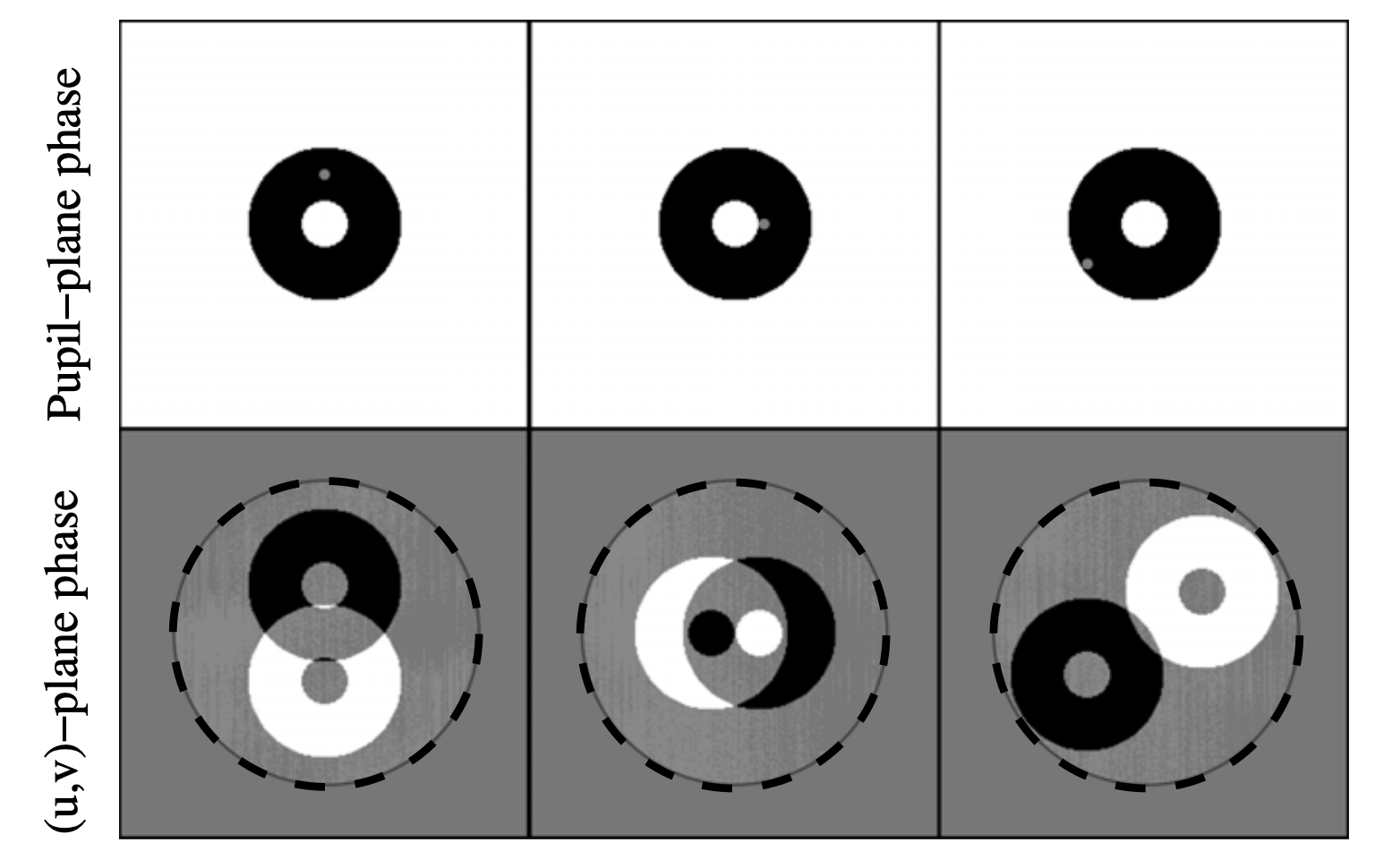
Jacobian of Palomar PHARO camera wrt phase

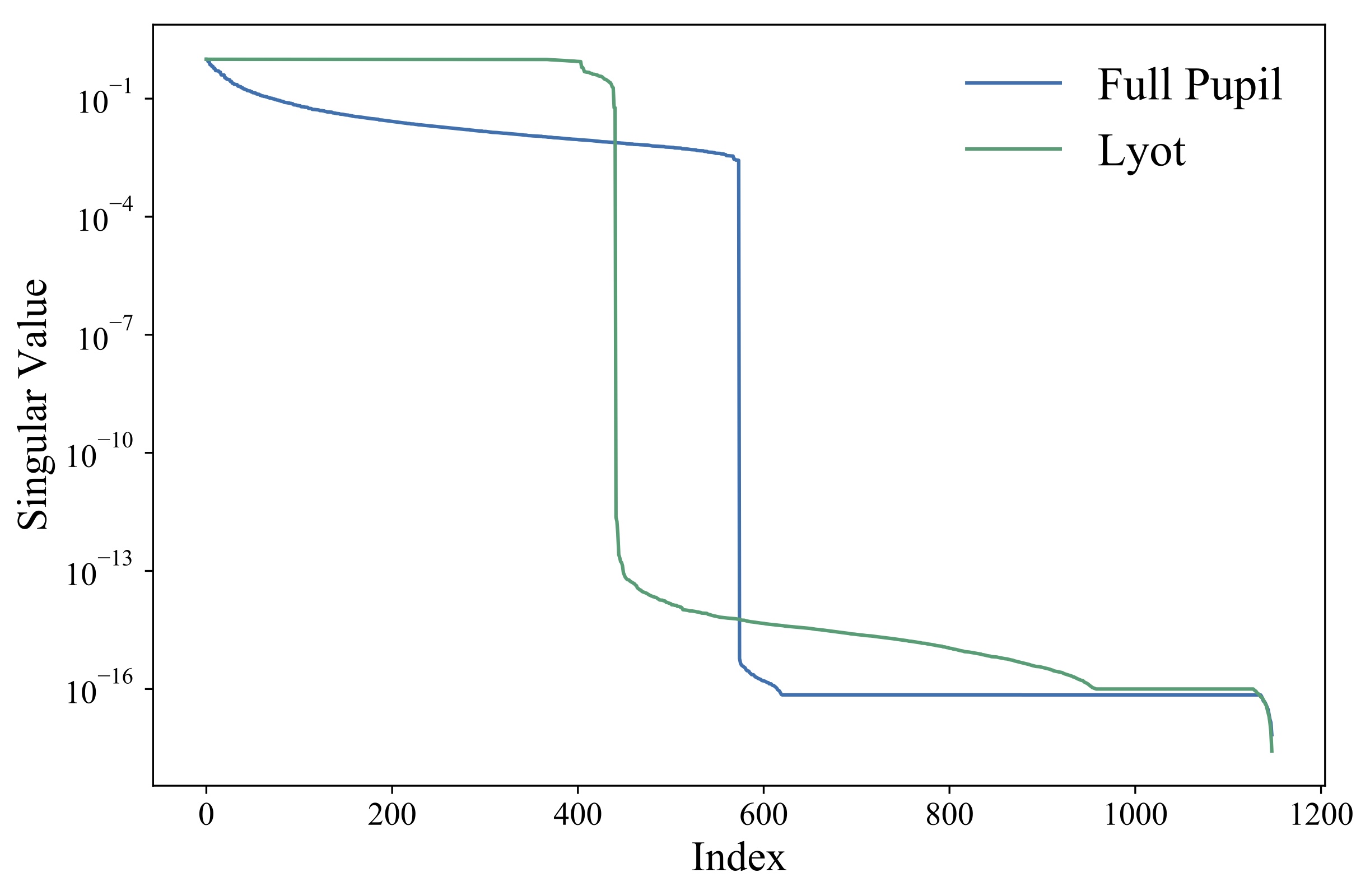
Extending kernel phase to coronagraphy has the same feature of a noise-corrupted space and a kernel space Singular values

The Future

Get using morphine and read the paper!

What else can we use this for?

Spatial light modulator enabled technology!

Particle beams?